3 raisonnements qu’on ne vous apprend pas à l’école

La réflexion personnelle est l’école de la sagesse.

Baltasar Gracian y Morales

Au lycée, on apprend plusieurs types de raisonnements généraux utiles dans la résolution de nombreux problèmes :

  • Le raisonnement par l’absurde : Pour montrer la négation. Par exemple, il sert à montrer que 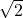\sqrt{2} n’est pas rationnel.
  • Le raisonnement par récurrence : Pour montrer qu’une propriété est vraie pour tout entier 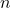n. Par exemple, il sert à montrer que pour tout entier n, \sum_{k=1}^nk^3=\left(\frac{n(n+1)}{2}\right)^2.
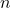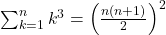  • Le raisonnement par contraposée : Pour montrer que 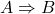A\Rightarrow B il est parfois plus simple de montrer que 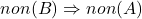non(B)\Rightarrow non(A). Par exemple, il sert à montrer que pour tout entier n, 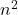n^2 pair implique 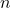n pair.
  • Le raisonnement par analyse-synthèse : Pour justifier l’existence/unicité d’une solution en déterminant sa tête. Par exemple, il sert à déterminer toutes les fonctions 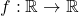f:\mathbb{R}\rightarrow\mathbb{R} dérivables telles que \forall x,y\in\mathbb{R} \quad f(x+y)=f(x)+f(y).

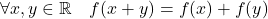Évidemment cette liste de raisonnements n’est pas exhaustive et je vous invite dans cet article à en découvrir trois autres !

Le principe d’invariance

Il est très utile lorsque vous avez un problème qui part d’une situation initiale, qui répète une même action à chaque étape pour passer à la situation suivante et qu’on vous demande s’il est possible d’aboutir à une situation finale donnée. Si vous arrivez alors à trouver une quantité qui n’est pas modifiée à chaque étape, autrement dit un invariant, et que cet invariant n’est pas le même pour la situation initiale et la situation finale alors forcément c’est impossible !

Exercice : Vous avez une liste d’entiers de 1 à 2024. A chaque étape, vous choisissez deux entiers dans cette liste, vous les effacez et vous écrivez à la place leur somme ou leur différence. A chaque étape, le nombre d’entiers de votre liste diminue donc de 1. Est-il possible qu’à la fin du processus, le dernier entier que vous obteniez soit 1 ?

✏A vous de jouer ! N’hésitez pas à prendre une feuille pour réfléchir à l’exercice.

On a une situation initiale : une liste d’entiers de 1 à 2024. On a une action qu’on effectue à chaque étape : Remplacer deux entiers par leur somme ou par leur différence. Et on a une situation finale : une liste constituée uniquement du chiffre 1.

Pour voir si c’est possible de passer de la situation initiale à la situation finale, on va donc essayer de trouver un invariant. L’une des difficultés ici est qu’on peut faire 2 types d’action :

  • Remplacer 2 entiers par leur somme
  • Remplacer 2 entiers par leur différence

Si on avait que la première possibilité, ce serait facile de trouver un invariant : on peut prendre la somme de tous les entiers de la liste. Cette somme serait de 1+2+\ldots+2024=\frac{2024\times2025}{2} au début et ne serait pas modifiée à chaque étape.

Mais vu qu’ici on peut faire une soustraction qui modifie cette somme, cela ne fonctionne pas. Néanmoins regardons comment la somme S_n à l’étape n est modifiée à l’étape n+1 lorsqu’on choisit la différence. Si on enlève des entiers a et b et qu’on les remplace par leur différence, on a

    \[S_{n+1} = S_n - a -b+(a-b) = S_n-2b.\]

On remarque donc qu’elle diminue forcément d’une quantité paire. Le voici notre invariant ! La parité de S_n i.e. la somme de tous les entiers de la liste. Cette parité ne change pas qu’on choisisse la somme ou la différence. Or, dans la situation initiale on a S_0=\frac{2024\times2025}{2}=1012\times 2025 qui est paire et dans la situation finale on a S_{final}=1 qui est impaire. C’est donc impossible d’aboutir à cette situation finale !

Le principe des tiroirs

L’idée de ce principe est extrêmement simple :

Si vous rangez (n+1) chaussettes dans n tiroirs, alors au moins un tiroir contient 2 chaussettes.

Malgré l’évidence de ce principe, il a de nombreuses applications non triviales car il n’est pas toujours facile de repérer ce que sont les tiroirs et ce que sont les chaussettes !

Exercice : Il y a n personnes dans une pièce. Montrer qu’il y a au moins deux personnes qui ont le même nombre de connaissances dans la pièce.

✏A vous de jouer ! N’hésitez pas à prendre une feuille pour réfléchir à l’exercice.

Ici, les chaussettes sont les personnes et les tiroirs sont le nombre de connaissances. Les tiroirs sont donc numérotés de 0 à n-1. Il y a n tiroirs et n personnes, donc pas de problème ? Il faut pousser un petit peu plus loin. S’il y a une personne dans le tiroir numéro 0, cela signifie qu’elle ne connaît personne. S’il y a une personne dans le tiroir numéro n-1, cela signifie qu’elle connaît toutes les autres personnes. C’est donc impossible d’avoir à la fois une personne dans le tiroir 0 et une personne dans le tiroir n-1 ! Il y a donc forcément 2 personnes dans le même tiroir et donc deux personnes ayant le même nombre de connaissances.

La descente infinie

Ce raisonnement est un peu plus spécifique mais vous verrez qu’il nous sera très utile dans de futurs articles.

Il est utile pour montrer qu’une équation polynomiale n’a pas de solution entières positives. Son principe est le suivant : On montre l’implication :

« Si une équation est vérifiée par certains entiers positifs a,b,c,\ldots alors elle est aussi vérifiée par des entiers positifs a_1,b_1,c_1,\ldots qui sont strictement plus petits que a,b,c,\ldots. »

Si on arrive à montrer cela, alors on peut répéter cette implication et en déduire à nouveau que s’il existe une solution alors il existe des entiers positifs a_2,b_2,c_2,\ldots encore plus petits, et on peut continuer comme cela indéfiniment. Mais c’est absurde car une suite d’entiers positifs ne peut pas strictement décroître indéfiniment ! Cela signifie donc qu’il n’y a pas de solutions entières positives.

Exercice : Montrer qu’il n’existe aucun quadruplet d’entiers strictement positifs (a,b,c,d) vérifiant l’équation :

    \[a^2+b^2=3(c^2+d^2).\]

✏A vous de jouer ! N’hésitez pas à prendre une feuille pour réfléchir à l’exercice.

Supposons qu’on ait une telle solution (a,b,c,d). On a 3|a^2+b^2, de cela on peut déduire que 3|a et 3|b en étudiant les congruences modulo 3 par exemple. En effet un carré d’entier ne peut être congru qu’à 0 ou 1 modulo 3 donc pour avoir 3|a^2+b^2 il faut forcément que 3|a^2 et 3|b^2 puis que 3|a et 3|b.

On a donc l’existence de a_1,b_1 entiers strictement positifs tels que a=3a_1 et b=3b_1. De plus

    \[a^2+b^2 = 9(a_1^2+b_1^2)=3(c^2+d^2).\]

Donc

    \[c^2+d^2=3(a_1^2+b_1^2).\]

Ainsi le quadruplet d’entiers strictement positifs (c,d,a_1,b_1) est une nouvelle solution de l’équation et est strictement plus petite que la solution (a,b,c,d). Par le principe de la descente infinie, c’est absurde ! Donc il n’y a pas de solution entières strictement positives.

Un commentaire

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Publications similaires