Pourquoi les nombres sont-ils beaux ? Cela revient à se demander pourquoi la neuvième symphonie de Beethoven est belle. Si vous ne voyez pas pourquoi, personne ne pourra vous l’expliquer. Je sais que les nombres sont beaux. S’ils ne sont pas beaux, rien ne l’est.
Paul Erdös

Dans l’épisode précédent, nous avions vu ce qu’était un nombre de Ramsey à travers une énigme qui nous a fait calculer ![]() . Essayons à présent de calculer
. Essayons à présent de calculer ![]() . Il s’agit de trouver le nombre minimal de sommets pour lequel on est sûr qu’un graphe contienne
. Il s’agit de trouver le nombre minimal de sommets pour lequel on est sûr qu’un graphe contienne ![]() sommets tous reliés entre eux ou
sommets tous reliés entre eux ou ![]() sommets isolés.
sommets isolés.
Interlude Vocabulaire
Introduisons un peu de vocabulaire pour que cela soit plus rapide à dire. Pour ![]() on appelle graphe complet à
on appelle graphe complet à ![]() sommets et on note
sommets et on note ![]() le graphe qui possède
le graphe qui possède ![]() sommets tous reliés entre eux. Dire qu’un graphe contient
sommets tous reliés entre eux. Dire qu’un graphe contient ![]() sommets tous reliés entre eux signifie donc que le graphe contient un
sommets tous reliés entre eux signifie donc que le graphe contient un ![]() .
.
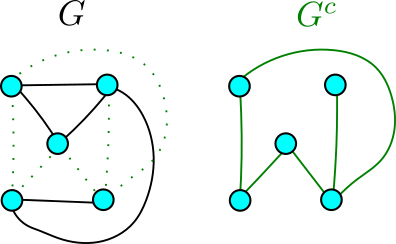
Pour ![]() un graphe, on appelle complémentaire de
un graphe, on appelle complémentaire de ![]() et on note
et on note ![]() le graphe avec les mêmes sommets que
le graphe avec les mêmes sommets que ![]() mais avec une arête entre deux sommets si et seulement si il n’y a pas d’arête entre ces deux sommets pour
mais avec une arête entre deux sommets si et seulement si il n’y a pas d’arête entre ces deux sommets pour ![]() (voir l’image ci-dessous pour bien comprendre).
(voir l’image ci-dessous pour bien comprendre).
Dire qu’un graphe contient ![]() sommets isolés revient donc à dire qu’il contient un
sommets isolés revient donc à dire qu’il contient un ![]() .
.

Plus généralement, on peut donc définir le nombre de Ramsey ![]() (pour
(pour ![]() entier) comme le nombre minimal de sommets pour lequel on est sûr qu’un graphe contienne un
entier) comme le nombre minimal de sommets pour lequel on est sûr qu’un graphe contienne un ![]() ou un
ou un ![]() .
.
Étape 1 : Comprendre la question
Nous avons déjà compris ce qu’était un nombre de Ramsey grâce à l’épisode précédent. Mais faisons le point sur ce qu’il va falloir faire pour calculer ![]() . Par définition de
. Par définition de ![]() , on doit pouvoir trouver un graphe avec
, on doit pouvoir trouver un graphe avec ![]() sommets tel qu’il n’ait pas de
sommets tel qu’il n’ait pas de ![]() et pas de
et pas de ![]() . Plus généralement, si on trouve un graphe avec
. Plus généralement, si on trouve un graphe avec ![]() sommets vérifiant cette dernière propriété, cela signifie que
sommets vérifiant cette dernière propriété, cela signifie que ![]() . Pour minorer
. Pour minorer ![]() nous allons donc devoir construire un tel graphe.
nous allons donc devoir construire un tel graphe.

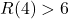
Pour ce qui est de la majoration, c’est différent. Pour montrer que ![]() , il faut s’assurer que pour tous les graphes à
, il faut s’assurer que pour tous les graphes à ![]() sommets, on trouve forcément un
sommets, on trouve forcément un ![]() ou un
ou un ![]() . Nous avons déjà vu que le nombre de graphe à
. Nous avons déjà vu que le nombre de graphe à ![]() sommets devient très vite immense donc c’est inenvisageable de vraiment tous les regarder un par un. Il va falloir faire un raisonnement général comme nous l’avions fait pour
sommets devient très vite immense donc c’est inenvisageable de vraiment tous les regarder un par un. Il va falloir faire un raisonnement général comme nous l’avions fait pour ![]() . D’ailleurs, essayons de faire le même non ?
. D’ailleurs, essayons de faire le même non ?
Étape 2 : Utilisation de notre expérience
Il y a un problème par rapport à l’épisode précédent, la valeur de ![]() nous était donnée par l’énoncé. Il suffisait de vérifier que pour tout graphe à
nous était donnée par l’énoncé. Il suffisait de vérifier que pour tout graphe à ![]() sommets, on trouve un
sommets, on trouve un ![]() ou un
ou un ![]() . Ici on ne sait pas à l’avance ce que sera la bonne valeur. Il va falloir découvrir cette valeur au cours de notre raisonnement. Fixons donc
. Ici on ne sait pas à l’avance ce que sera la bonne valeur. Il va falloir découvrir cette valeur au cours de notre raisonnement. Fixons donc ![]() entier. On reprend le raisonnement de l’épisode précédent.
entier. On reprend le raisonnement de l’épisode précédent.
Supposons par l’absurde qu’il existe un graphe ![]() à
à ![]() sommets ne contenant pas de
sommets ne contenant pas de ![]() et pas de
et pas de ![]() . Regardons l’un de ses sommets
. Regardons l’un de ses sommets ![]() et voyons comment il est relié aux autres sommets.
et voyons comment il est relié aux autres sommets.
Si on regarde bien le raisonnement qu’on avait effectué, ce qui nous permettait de trancher c’était soit que le nombre de sommets auxquels ![]() était relié était trop grand ou bien le nombre de sommets auxquels
était relié était trop grand ou bien le nombre de sommets auxquels ![]() n’était pas relié était trop grand. Notons donc
n’était pas relié était trop grand. Notons donc ![]() l’ensemble des sommets reliés à
l’ensemble des sommets reliés à ![]() et
et ![]() l’ensemble des sommets non reliés à
l’ensemble des sommets non reliés à ![]() .
.
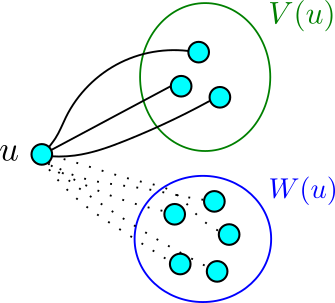
Que signifie ici ![]() trop grand ? Dans la preuve pour
trop grand ? Dans la preuve pour ![]() , cela signifiait simplement qu’on pouvait trouver une arête ou, autrement dit, un
, cela signifiait simplement qu’on pouvait trouver une arête ou, autrement dit, un ![]() . De la même façon ici, cela signifie qu’on peut trouver un
. De la même façon ici, cela signifie qu’on peut trouver un ![]() dans
dans ![]() . En effet si cela est le cas, alors ce
. En effet si cela est le cas, alors ce ![]() avec le
avec le ![]() , auquel ils sont tous reliés par définition, ferait que nous pouvons trouver un
, auquel ils sont tous reliés par définition, ferait que nous pouvons trouver un ![]() ce qui serait absurde.
ce qui serait absurde.
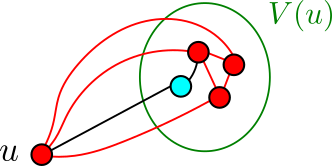
A partir de quelle taille on est sûr de trouver un ![]() ? La première réponse qui vient peut être c’est à partir d’un nombre
? La première réponse qui vient peut être c’est à partir d’un nombre ![]() de sommets, mais ce n’est pas tout à fait correct. En fait, un nombre
de sommets, mais ce n’est pas tout à fait correct. En fait, un nombre ![]() de sommets assure l’existence d’un
de sommets assure l’existence d’un ![]() ou d’un
ou d’un ![]() , mais si seule l’option
, mais si seule l’option ![]() est cochée, cela ne nous aide pas. Mmm… Si on regarde bien à nouveau le raisonnement de l’épisode précédent, ce qu’on aimerait dans notre cas c’est un nombre de sommets qui assure l’existence d’un
est cochée, cela ne nous aide pas. Mmm… Si on regarde bien à nouveau le raisonnement de l’épisode précédent, ce qu’on aimerait dans notre cas c’est un nombre de sommets qui assure l’existence d’un ![]() ou d’un
ou d’un ![]() . En effet, par notre hypothèse par l’absurde, on ne pourrait alors pas avoir de
. En effet, par notre hypothèse par l’absurde, on ne pourrait alors pas avoir de ![]() et on serait forcé d’avoir un
et on serait forcé d’avoir un ![]() . C’est vrai que jusque là on a toujours regardé les nombres de Ramsey avec le même entier
. C’est vrai que jusque là on a toujours regardé les nombres de Ramsey avec le même entier ![]() pour
pour ![]() et
et ![]() mais rien ne nous empêche de casser cette symétrie !
mais rien ne nous empêche de casser cette symétrie !
Étape 3 : Généraliser pour simplifier
Pour ![]() entiers, on définit le nombre de Ramsey
entiers, on définit le nombre de Ramsey ![]() comme le nombre minimal de sommets d’un graphe nécessaire pour être sûr qu’il contienne un
comme le nombre minimal de sommets d’un graphe nécessaire pour être sûr qu’il contienne un ![]() ou un
ou un ![]() . Muni de cette définition, si
. Muni de cette définition, si ![]() comporte
comporte ![]() sommets alors cela signifie, puisque notre hypothèse impose qu’il n’y ait pas de
sommets alors cela signifie, puisque notre hypothèse impose qu’il n’y ait pas de ![]() , qu’on a forcément un
, qu’on a forcément un ![]() dans
dans ![]() et donc un
et donc un ![]() dans
dans ![]() . C’est absurde ! On doit donc forcément avoir
. C’est absurde ! On doit donc forcément avoir ![]() .
.
Il faudra évidemment pouvoir calculer ce ![]() mais continuons pour l’instant notre raisonnement qui a l’air de fonctionner de façon assez générale.
mais continuons pour l’instant notre raisonnement qui a l’air de fonctionner de façon assez générale.
Que signifie ![]() trop grand ? Si vous avez bien suivi, cela arrive quand
trop grand ? Si vous avez bien suivi, cela arrive quand ![]() comporte
comporte ![]() sommets. En effet, notre hypothèse impose de ne pas avoir de
sommets. En effet, notre hypothèse impose de ne pas avoir de ![]() donc on a forcément un
donc on a forcément un ![]() dans
dans ![]() . Mais par définition de
. Mais par définition de ![]() , on sait aussi que
, on sait aussi que ![]() est isolé de ce
est isolé de ce ![]() et il forme donc avec celui-ci un
et il forme donc avec celui-ci un ![]() . C’est absurde ! On doit donc forcément avoir
. C’est absurde ! On doit donc forcément avoir ![]() .
.

Finalement on a réussi à majorer le nombre de sommets de notre graphe, notons ce nombre ![]() . On a
. On a
![]()

Dès qu’on dépasse ce nombre de sommets, on est sûr de trouver un ![]() ou un
ou un ![]() . Cela signifie donc qu’on a montré que
. Cela signifie donc qu’on a montré que
![]()
En fait, ce raisonnement peut se faire pour le cas général exactement de la même façon. On a la propriété suivante, dont la preuve est laissée au lecteur comme exercice de compréhension :
![]()
Étape 4 : Calcul de R(3,4)
Je vous laisse encore un exercice de compréhension (eh ouais au boulot un peu !) : Montrer que ![]() en se servant du graphe complémentaire.
en se servant du graphe complémentaire.
Il nous faut donc seulement calculer ![]() .
.
Majoration de R(3,4)
En se servant du résultat général précédent on a
![]()
On connaît la valeur de ![]() grâce à l’épisode précédent, elle est de
grâce à l’épisode précédent, elle est de ![]() .
.
Pour ![]() il s’agit de s’avoir à partir de quel nombre de sommets on est sûr qu’un graphe contienne une arête ou
il s’agit de s’avoir à partir de quel nombre de sommets on est sûr qu’un graphe contienne une arête ou ![]() sommets isolés. On peut avoir un graphe constitué de
sommets isolés. On peut avoir un graphe constitué de ![]() sommets isolés qui ne contient donc ni arête ni
sommets isolés qui ne contient donc ni arête ni ![]() sommets isolés mais dès qu’un graphe a
sommets isolés mais dès qu’un graphe a ![]() sommets c’est impossible d’éviter cela. Il est donc clair que
sommets c’est impossible d’éviter cela. Il est donc clair que ![]() .
.
Finalement on a donc
![]()
Minoration de R(3,4)
Idéalement on aimerait bien que ce soit la majoration optimale, c’est-à-dire qu’on ait en fait ![]() . Mais pour s’assurer de cela, il faut construire un graphe à
. Mais pour s’assurer de cela, il faut construire un graphe à ![]() sommets ne contenant pas de
sommets ne contenant pas de ![]() et pas de
et pas de ![]() .
.
Faisons cela étape par étape en commençant par un peu moins de sommets. Disons ![]() sommets étant donné qu’on sait déjà que
sommets étant donné qu’on sait déjà que ![]() .
.
Une façon qui me vient de faire un graphe sans triangle c’est de simplement relier les sommets entre eux en cercle.

Pour ![]() sommets, cela fonctionne. Il n’y a pas de triangles et il n’y a pas
sommets, cela fonctionne. Il n’y a pas de triangles et il n’y a pas ![]() sommets isolés. Pour
sommets isolés. Pour ![]() sommets cela fonctionne aussi.
sommets cela fonctionne aussi.

Par contre en faisant pareil à ![]() sommets, on peut trouver
sommets, on peut trouver ![]() sommets isolés.
sommets isolés.

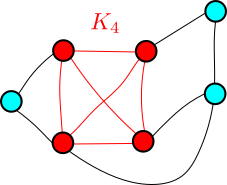
On va donc ajouter des arêtes, sans créer de triangle, pour rompre ces isolements. Si on relie deux sommets séparés de ![]() , cela crée immédiatement un triangle. On peut par contre relier les sommets rouges opposés qui ne sont alors plus isolés, par contre les sommets bleus sont toujours isolés.
, cela crée immédiatement un triangle. On peut par contre relier les sommets rouges opposés qui ne sont alors plus isolés, par contre les sommets bleus sont toujours isolés.

On répète donc l’opération avec eux et on obtient le graphe suivant :
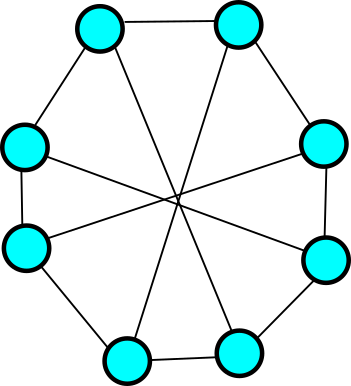
On voit que ce graphe n’a pas de triangle et n’a pas non plus ![]() sommets isolés. On a donc
sommets isolés. On a donc ![]() .
.
Plus qu’à traiter le graphe à neuf sommets et c’est gagné. En faisant la même stratégie, on se rend compte que le sommet supplémentaire pose vraiment problème.

Bon on est un peu embêtés… On continue à faire des dessins et à essayer de tracer des arêtes sans créer de triangles et sans avoir quatre sommets isolés mais rien à faire, on n’y arrive pas… Est-ce vraiment possible ? Peut être que finalement la majoration ![]() de tout à l’heure n’est pas optimale ?
de tout à l’heure n’est pas optimale ?
Retour sur la majoration de R(3,4)
Supposons que ![]() et regardons plus précisément ce que cela implique. Par définition de
et regardons plus précisément ce que cela implique. Par définition de ![]() , il existe alors un graphe
, il existe alors un graphe ![]() avec
avec ![]() sommets et qui n’a ni
sommets et qui n’a ni ![]() ni
ni ![]() . Prenons comme précédemment un sommet
. Prenons comme précédemment un sommet ![]() de
de ![]() . En reprenant notre raisonnement sur la majoration, on voit qu’on doit alors forcément avoir
. En reprenant notre raisonnement sur la majoration, on voit qu’on doit alors forcément avoir ![]() et
et ![]() .
.

Que peut-on tirer de plus que tout à l’heure …? En y réfléchissant, c’est assez fort ce que l’on dit car on a précisément ces égalités pour tout sommet ![]() de notre graphe
de notre graphe ![]() . Les
. Les ![]() sommets de notre graphe sont tous reliés à exactement
sommets de notre graphe sont tous reliés à exactement ![]() sommets, ces
sommets, ces ![]() sommets étant en plus isolés. Qu’est-ce cela nous donne comme information sur notre graphe …? Mmm… Peut-on connaître le nombre d’arêtes de notre graphe par exemple ? Oui on peut ! On vient de dire que chaque sommet est relié à exactement
sommets étant en plus isolés. Qu’est-ce cela nous donne comme information sur notre graphe …? Mmm… Peut-on connaître le nombre d’arêtes de notre graphe par exemple ? Oui on peut ! On vient de dire que chaque sommet est relié à exactement ![]() autres sommets, autrement dit il y a précisément
autres sommets, autrement dit il y a précisément ![]() arêtes reliées à chaque sommet. Il faut faire attention à ne pas les compter
arêtes reliées à chaque sommet. Il faut faire attention à ne pas les compter ![]() fois car chaque arête est reliée à exactement
fois car chaque arête est reliée à exactement ![]() sommets.
sommets.

Puisqu’il y a ![]() sommets, le nombre d’arêtes de notre graphe est donc censé être
sommets, le nombre d’arêtes de notre graphe est donc censé être
![]()
mais ce n’est pas un nombre entier ça ! C’est absurde ! En vérifiant à nouveau notre décompte d’arêtes, on se convainc bien qu’on aboutit à une contradiction en supposant que ![]() . Finalement on a donc
. Finalement on a donc ![]() . Et en combinant avec notre minoration, on déduit finalement le résultat
. Et en combinant avec notre minoration, on déduit finalement le résultat
![]()
Étape 5 : Calcul de R(4)
Majoration de R(4)
On a toujours la majoration du résultat général précédent :
![]()
On espère que cette majoration sera suffisante vu que ce n’était pas si simple à améliorer pour ![]() .
.
Minoration de R(4)
Idéalement, on aimerait réussir à construire un graphe à 17 sommets sans ![]() et sans
et sans ![]() . On commence comme avant à faire une structure en cercle.
. On commence comme avant à faire une structure en cercle.

Essayons de rajouter le plus possible d’arêtes sans créer de ![]() . On n’a plus de problème en créant des
. On n’a plus de problème en créant des ![]() et on peut donc mettre une arête tous les deux sommets.
et on peut donc mettre une arête tous les deux sommets.

On ne peut pas mettre une arête tous les 3 sommets par contre. Par exemple en mettant une arête entre le sommet 1 et le sommet 4, on crée un ![]() avec les sommets 1,2,3 et 4. On continue donc en mettant une arête tous les quatre sommets.
avec les sommets 1,2,3 et 4. On continue donc en mettant une arête tous les quatre sommets.

On voit qu’il nous reste toujours beaucoup de sommets isolés, il y en a 5 en rouge par exemple. Essayons de casser l’isolement de ces sommets rouge. On ne peut pas tracer une arête entre 1 et 4 sinon ça crée un ![]() avec les sommets 1,3,5 et 7. On va donc tracer une arête entre 1 et 10 puis tous les neuf sommets.
avec les sommets 1,3,5 et 7. On va donc tracer une arête entre 1 et 10 puis tous les neuf sommets.

On obtient un magnifique graphe et on peut vérifier que celui-ci ne contient pas de ![]() et ne contient pas non plus de
et ne contient pas non plus de ![]() . On a donc
. On a donc ![]() et donc finalement
et donc finalement ![]() !
!
Conclusion
Eh ben dis donc c’était pas de tout repos mais on y est parvenu ! On sent que ça se complique mais on ne sent pas encore vraiment pourquoi ![]() serait si compliqué à calculer. On n’est plus si loin finalement, il faudrait
serait si compliqué à calculer. On n’est plus si loin finalement, il faudrait ![]() et puis juste après vient
et puis juste après vient ![]() . On verra dans le prochain épisode que ce n’est hélas pas si simple…
. On verra dans le prochain épisode que ce n’est hélas pas si simple…
En tout cas j’espère que ce tout premier article piste rouge du blog vous a plu et je vous dis à très bientôt pour la suite =)