La philosophie est un jeu avec un but et pas de règles. Les mathématiques sont un jeu avec des règles mais pas de but.
Gian Carlo Rota
Aujourd’hui, je vous présente un jeu mathématique proposé par le médaillé Fields Maxim Kontsevich. Le jeu s’appelle « Pebbling a Chessboard » en anglais. Le principe est le suivant :
Vous avez un échiquier infini dans le quart de plan. Les 
cases du coin sont appelées la prison et au début du jeu il y a pions dessus. Le but est de réussir à retirer les pions de cette prison.
Pour cela, vous pouvez déplacer les pions uniquement de la façon suivante : Lorsqu’un pion a sa case de droite et sa case du dessus inoccupées, il peut disparaître et se dédoubler sur ces deux cases.
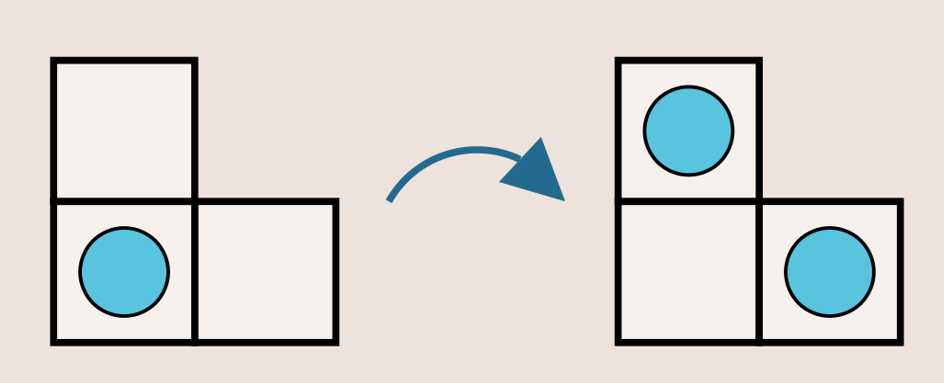
Est-il possible de libérer les pions de la prison ?
✏A vous de jouer ! N’hésitez pas à prendre une feuille ou un échiquier pour réfléchir !
Solution
Après plusieurs tentatives pour essayer de libérer les pions sans y parvenir, on commence à se dire que c’est sans doute impossible… Comment le prouver ?
On est dans un exemple typique d’utilisation du principe d’invariance (voir article sur les 3 raisonnements non appris en cours). On a une situation initiale : un échiquier avec pions dans la prison. On a une action à réaliser à chaque étape : dédouble un pion comme expliqué plus haut. Et on a une situation finale : un échiquier sans pion sans la prison.
Une façon de montrer l’impossibilité de résoudre ce jeu est donc de trouver un invariant i.e. une quantité qui n’est pas modifiée à chaque action. Ici l’invariant n’apparait pas clairement mais ce n’est pas grave, on va le construire nous-mêmes. Donnons une valeur à chacune des cases de l’échiquier. Lorsqu’on effectue une action, que se passe-t-il ?
On perd la valeur 
et on gagne les valeurs 
et 
. Ainsi, si on prend comme invariant la somme des cases sur lesquelles il y a un pion et qu’on note 
cette somme à l’étape 
, on a
![\[S_{n+1} = S_n-x+(y+z).\]](https://mathrais.fr/wp-content/ql-cache/quicklatex.com-8761b19f1d871b12ef4348c2ee4c5cc1_l3.png "Rendered by QuickLaTeX.com")
On aimerait donc que 
pour que la somme ne change pas à chaque étape. De plus, par symétrie, on peut prendre 
. On veut donc que 
c’est à dire que chaque case soit le double des cases qui sont à droite et au dessus.
En prenant arbitrairement la valeur simple de 
pour la première case de l’échiquier, on obtient cette attribution pour les cases :
Dans la situation initiale, il y a pions dans la prison donc on a 
.
Dans la situation finale, la somme est maximale si toutes les cases, sauf celles de la prison, sont occupées par des pions. En addition toutes ces cases (plusieurs sommes géométriques à faire), on obtient après calcul que cela vaut aussi 
.
On n’a a priori pas de contradiction… Il faut en fait remarquer qu’avoir toutes les cases occupées par des pions c’est impossible. En effet, gagner le jeu ça veut dire le gagner en un nombre fini d’actions. Il y aura donc un nombre fini de cases occupées par les pions et donc une somme 
, on a donc bien une contradiction !
Conclusion : Il est impossible de libérer les pions.
Pour aller plus loin
On peut se demander ce qu’il se passe lorsqu’on modifie la taille et/ou la forme de la prison. Il y a alors plein de choses intéressantes à dire et je vous invite à consulter les deux articles suivants si cela vous intéresse :
- https://mathweb.ucsd.edu/~fan/mypaps/fanpap/150chess.pdf
- https://www.sciencedirect.com/science/article/pii/S0895717707001203
