Le Théorème de Thalès

Rien n’est plus facile à apprendre que la géométrie pour peu qu’on en ait besoin.
Sacha Guitry

Après avoir traité Pythagore, on s’intéresse à l’autre fameux résultat de géométrie : le théorème de Thalès. Il est souvent moins bien retenu alors qu’il confirme quelque chose de très naturel. Imaginez que vous ayez construit un triangle.

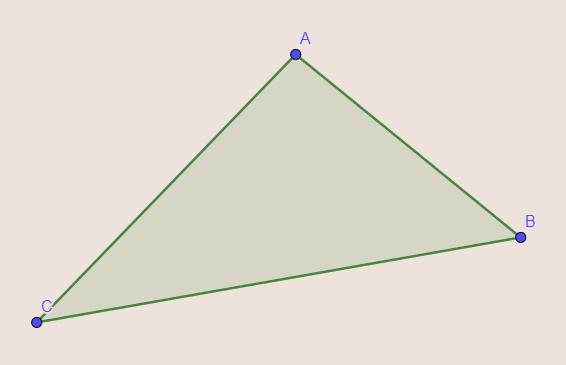
Vous vous dîtes que finalement il n’a pas la bonne taille. Vous aimeriez un triangle deux fois plus grand tout en gardant la « même apparence ». Par « même apparence », on veut dire qu’on veut conserver la valeur des trois angles de notre triangle. Deux triangles de « même apparence » s’appellent des triangles semblables. Mais qu’est-ce qu’un triangle deux fois plus grand ? Là vous vous dîtes sans doute qu’il suffit de doubler chaque longueur du triangle et vous avez raison, mais est-ce si évident ? Si je double la longueur d’un seul côté et que je reforme un triangle semblable à celui d’avant, suis-je sûr que ses deux autre côtés auront aussi doublé de longueur ?

Le théorème de Thalès affirme justement que la réponse à cette question est oui. Plus généralement la réponse est oui pas juste pour une multiplication de la taille par $2$ mais pour une multiplication de la taille par un réel $\alpha\geq 0$ .

Voyons voir comment on peut prouver un tel résultat.

✏A vous de jouer ! N’hésitez pas à prendre une feuille de papier pour réfléchir à la question.

Étape 1 : Simplifier le problème

On regarde le dessin plus haut et on a un peu de mal à trouver une idée… Ce qu’on fait dans ce cas c’est d’essayer de résoudre un problème plus simple. Ici, on peut par exemple essayer avec des triangles particuliers. Le triangle équilatéral peut être un bon premier essai étant donné que tous ses côtés devront être égaux. Faisons donc le dessin avec un triangle équilatéral.

Dans ce cas là, on peut déjà remarquer qu’on a une symétrie par rapport à la hauteur passant par $A$ et donc il est clair que $AD=AE$ . Il reste à voir pourquoi $DE=AD=AE$ . Mmm… Décidément ce n’est pas évident. Simplifions encore et regardons le cas du triangle équilatéral avec $AD$ qui est exactement le double de $AB$ . Dans ce cas là, on voit que le grand triangle peut se décomposer en quatre petits triangles équilatéraux identiques.

Il est alors clair que $DE=2DF=2DB=2AB$ . Mais bon c’est un cas très spécifique. Peut-on quand même reprendre cette idée de décomposer le grand triangle en petits triangles ? Revenons avec notre triangle équilatéral dont une longueur est multipliée par $\alpha$ (et non forcément $\alpha=2$ ).

Bon les triangles ne sont pas identiques et ça n’a pas l’air de nous aider plus que cela. Poussons néanmoins le raisonnement et étudions les aires de ces triangles étant donné qu’il y a cette histoire de recouvrement. Notons $h=GF$ et $h'=AG$ . L’aire du triangle $BDF$ est la même que celle du triangle $CFE$ et est égale à

$\frac{\text{base}\times\text{hauteur}}{2} = \frac{DF\times h}{2}$

L’aire du triangle $BCF$ est $\frac{BC\times h}{2}$ . Finalement on a deux façons de calculer l’aire du grand triangle.

$Aire(ADE)=Aire(ABC)+2Aire(BDF)+Aire(BCF)$

D’où

$\frac{DE\times(h+h')}{2}=\frac{BC\times h'}{2}+2\frac{DF\times h}{2}+\frac{BC\times h}{2}$

Donc en simplifiant et en se servant du fait que $2DF=DE$ , on trouve

$h'DE=(h+h')BC$

Finalement

$\frac{BC}{DE}=\frac{h'}{h+h'}$

On n’a pas encore ce qu’on voulait mais on a quand même quelque chose d’intéressant. Le rapport de la hauteur du petit triangle sur la hauteur du grand triangle est égale au rapport de $BC$ sur $DE$ . C’est d’autant plus intéressant que cette idée de diviser le triangle en deux par une hauteur peut être utilisé de façon très générale.

Étape 2 : Retour au cas général

On revient au cas général alors qu’on n’a pas fini le cas particulier ?! En fait si on récapitule, on a vu que pour conclure sur le triangle équilatéral, il suffisait d’étudier un schéma du type ci-dessous.

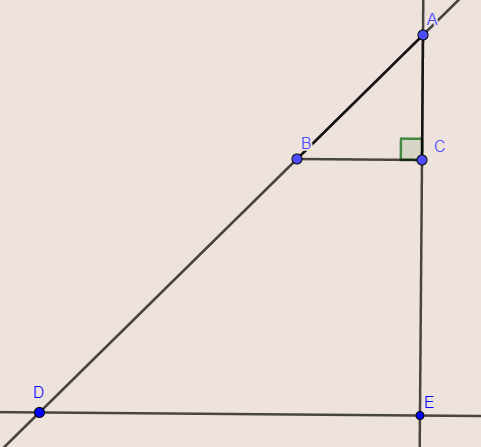
En fait même pour un triangle quelconque on retrouve ce schéma en divisant le triangle en deux avec sa hauteur.

On a vu que pour lier $\frac{AC}{AE}$ à $\frac{BC}{DE}$ il suffisait de regarder les aires des triangles $DBE,BCE$ et $ABC$ . Refaisons le raisonnement pour être sûr.

L’aire du triangle $DBE$ est égale à $\frac{CE\times DE}{2}$ . L’aire du triangle $BCE$ est égale à $\frac{BC}{CE}{2}$ . Et enfin l’aire du triangle $ABC$ est $\frac{AC}{BC}{2}$ . On a donc l’égalité

$Aire (ADE) = Aire(ABC)+Aire(DBE)+Aire(BCE)$

qui devient

$\frac{AE\timesDE}{2} = \frac{AC\timesBC}{2}+\frac{CE\times DE}{2}+\frac{BC\timesCE}{2}.$

D’où

$DE(AC-CE)=BC(AC+CE).$

Donc finalement

$\frac{BC}{DE}=\frac{AC}{AE}$

comme attendu. Il ne nous reste maintenant qu’à montrer que ce rapport est aussi égal au rapport $\frac{AB}{AD}$ . Si on réfléchit, ce qui nous permettait de faire intervenir $AC$ et $AE$ dans ce calcul d’aires était le fait que ce soit des hauteurs (ou bases) de triangles. On ne voit pas trop comment $AB$ et $AD$ pourraient être des hauteurs car il n’y a pas d’angle droit de ce côté là. Faisons donc en sorte que ce soit des bases de triangles.

On a besoin d’introduire la hauteur $HC$ issue de $C$ . Le problème c’est qu’on a envie que cette hauteur disparaisse dans les calculs ensuite… Dans quels calculs d’aire intervient-elle ? Elle intervient dans l’aire du triangle $ABC$ égale à $\frac{AB\times HC}{2}$ et dans l’aire du triangle $DAC$ égale à $\frac{DA\times HC}{2}$ . On aimerait donc faire le rapport de ces aires pour que cette hauteur disparaisse :

$\frac{Aire(ABC)}{Aire(DAC)}=\frac{AB}{AD}$

Eh mais attendez ! C’est super intéressant ça non ?! On vient de transformer un rapport d’aire en un rapport de longueur ! Est-ce qu’on peut faire pareil avec les autres rapports qui nous intéressent ?

Oui tout à fait, par exemple

$\frac{Aire(DBC)}{Aire(DCE)}=\frac{\frac{BC\times CE}{2}}{\frac{DE\times CE}{2}}= \frac{BC}{DE}$

$\frac{Aire(ABC)}{Aire(ABE)}=\frac{\frac{AC\times BC}{2}}{\frac{AE\times BC}{2}}= \frac{AC}{AE}.$

On voit que l’aire du triangle $ABC$ intervient dans le premier et le troisième rapport, en fait il nous suffit de montrer qu’on a $Aire(DAC)=Aire(ABE)$ pour conclure. Mais c’est clair en fait vu qu’ils ont le triangle $ABC$ en commun et que l’aire des triangles $DBC$ et $BCE$ sont égales puisqu’elles ont une base commune $BC$ et la même hauteur puisque $D$ et $E$ sont sur une droite parallèle à $BC$ . Finalement

$Aire(DAC)=Aire(ABE)$$

Puis on déduit

$\frac{AB}{AD}=\frac{AC}{AE}= \frac{BC}{DE}.$

Pour le triangle général (et pas juste le triangle rectangle, moitié du triangle principal), il suffit d’appliquer le même raisonnement sur l’autre moitié et on déduit le théorème de Thalès.

Conclusion

Ainsi le théorème de Thalès affirme un résultat naturel mais pas si évident à montrer comme on a pu le constater.

On peut se poser la question de la réciproque : Si on a un triangle $ABC$ et que l’on prolonge le côté $AB$ et le côté $AC$ de telle sorte que $\frac{AB}{AD}=\frac{AC}{AE}$ alors est-ce que les triangles $ABC$ et $ADE$ sont semblables, autrement dit est-ce que la droite $DE$ et la droite $BC$ sont parallèles ?

La réponse à cette question est oui et cela s’appelle la réciproque du théorème de Thalès.

Étape 1 : Simplifier le problème

Étape 2 : Retour au cas général

Conclusion

Laisser un commentaireAnnuler la réponse

Publications similaires

Calculer une racine carrée sans calculatrice – La méthode d’Héron

Kangourou des Maths – 6ème/5ème 2023 – Correction détaillée

Les ponts de Königsberg