Les nombres de Ramsey – Episode 1

Un problème digne d’attaque montre sa valeur en ripostant.

Paul Erdös

Ce premier épisode sur les nombres de Ramsey est plutôt piste bleue, mais étant donné que le reste de la série sera rouge, je préfère lui donner une couleur uniforme.

Il y a un exercice très classique qu’on propose souvent aux élèves intéressés préparant les Olympiades ou toute autre compétition de mathématiques. Derrière un énoncé assez simple et amusant se cache en fait l’un des concepts mathématiques les plus étudiés aujourd’hui. Mais avant d’aller plus loin, regardons donc cet exercice :

❔ Montrer que dans un groupe de six personnes, il existe toujours un groupe de trois personnes qui se connaissent toutes entre elles ou un groupe de trois personnes dont aucune ne se connait.

✏️ A vous de jouer ! Prenez le temps de réfléchir à ce premier problème d’une longue série !

Étape 1 : Comprendre la question

Cela prend déjà quelques relectures pour comprendre l’énoncé. On a un groupe de six personnes dont on ne sait rien. Elles peuvent toutes se connaître entre elles, ne pas du tout se connaître, cette personne peut connaître celle-ci mais cette autre personne pas celle-ci, etc. On sent déjà qu’on aimerait bien numéroter les personnes, disons de à . Le fait que ce soit des personnes n’a d’ailleurs pas d’importance, on peut les représenter par l’un des objets les plus simples des mathématiques : le point.

La seule information importante à propos de ces personnes est de savoir lesquelles se connaissent et lesquelles ne se connaissent pas. Riches de notre expérience sur Königsberg, on commence doucement à voir souvent des graphes et on va ainsi relier les points entre eux si les personnes se connaissent (et ne pas les relier si elles ne se connaissent pas).

Pour résumer, il s’agit donc d’un problème qui peut se modéliser par les graphes : des sommets reliés par des arêtes. La question est alors de savoir si dans tout graphe à sommets, il est possible de trouver sommets tous reliés entre eux ou de trouver sommets dont aucun n’est relié. Comme c’est un peu long à dire, on va appeler le fait de « trouver sommets tous reliés entre eux » : « trouver triangle ». 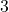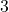Et on va appeler le fait de « trouver sommets dont aucun n’est relié » : « trouver sommets isolés ».

Étape 2 : Simplifier la question

Au fur à mesure des articles, on commence à se rendre compte que parfois simplifier la question c’est en fait la généraliser. Ici on peut se demander ce qui se passe en modifiant le nombre de sommets de notre graphe. On peut aussi modifier le fait qu’on recherche sommets reliés (ou isolés).

Baissons ces nombres au maximum. Si on recherche seulement sommet cela n’a aucun intérêt donc regardons ce qui se passe si on cherche sommets reliés ou sommets non reliés. C’est sans intérêt aussi car dès qu’on a deux sommets, on a bien l’un ou l’autre des cas.

Gardons donc le fait qu’on cherche bien sommets. On peut par contre jouer avec le nombre de sommets de notre graphe. On voit qu’avec un graphe à sommets le fait de pouvoir trouver triangle ou sommets isolés n’est pas assuré :

En faisant quelques dessins, on vérifie aussi que pour un graphe à sommets ainsi que pour un graphe à sommets ce n’est pas non plus assuré.

Finalement, si l’énoncé est juste, le graphe à sommets doit être le premier graphe pour lequel on est assuré que cela arrive. Comment allons-nous montrer cela ?

Étape 3 : S’attaquer au problème

Idée n°1 : Liste exhaustive

Une idée serait de faire une liste exhaustive de tous les graphes à sommets et de vérifier que, pour chacun d’eux, on est capable de trouver un triangle ou sommets isolés. Avant de partir dans cette liste, estimons combien il y a de graphes à sommets.

✏️ Exercice laissé au lecteur ! Combien y-a-t-il de graphes à sommets et plus généralement combien y a-t-il de graphes à sommets (où est un entier naturel) ?

Si vous avez calculé ce nombre, vous vous êtes rendus compte qu’il était plutôt grand. Un ordinateur pourrait sans doute faire le travail (pour sommets) mais bon ici on aimerait trouver plus simple. Comme souvent, il va falloir être plus malin que juste faire une liste.

Idée n°2 : Comprendre l’impossibilité

Pour comprendre pourquoi il va forcément y avoir un triangle ou points isolés, le mieux est sans doute d’essayer de créer un graphe à sommets ne vérifiant pas cela. On espère alors se rendre compte que c’est impossible. Dans cette logique, nous allons essayer un raisonnement par l’absurde.

Supposons donc, par l’absurde, qu’il existe un graphe à sommets sans triangle et sans points isolés. Regardons l’un de ses sommets et comment il est relié aux autres sommets.

• Si 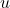n’est pas relié à un autre sommet. Alors on sent qu’on a un bon début pour trouver 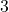points isolés. En effet 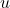est alors isolé de tous les autres points et puisqu’il n’y a pas 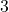points isolés dans le graphe, cela signifie forcément que tous les autres points doivent être reliés entre eux. Or cela implique qu’on puisse trouver un triangle, c’est absurde.

• Si 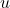est relié à exactement 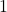sommet. De même que pour le cas précédent, cela implique que les 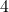autres sommets, auxquels 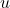n’est pas relié, doivent être tous liés entre eux. Donc on peut trouver un triangle, c’est absurde.

• Si 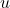est relié à exactement 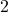sommets. Alors on a à nouveau le même raisonnement avec les 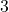sommets auxquels 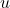n’est pas relié, on aboutit donc encore à une contradiction.

• Si 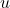est relié à exactement 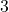sommets. Cette fois-ci, on s’approche plus de l’existence d’un triangle que de 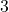points isolés. En fait les 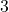sommets auxquels 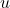est relié n’ont plus le droit d’avoir de liaison entre eux car sinon on a un triangle (formé de 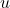et de deux sommets reliés). Mais cela signifie alors que ces 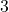points sont isolés ! C’est absurde.

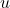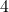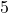• Si est relié à ou sommets, le même raisonnement que le cas précédent montre une absurdité.

Finalement, tous les cas sont impossibles et donc notre hypothèse de départ est forcément fausse. On en déduit que a forcément un triangle ou points isolés. On a donc réussi à montrer ce que nous demandait l’exercice !

Conclusion

Notons que pour les graphes qui ont plus de sommets, on aura aussi forcément l’existence d’un triangle ou de points isolés (il suffit pour cela de considérer un sous-graphe à sommets dans ces graphes, celui-ci a forcément un triangle ou points isolés par le résultat précédent). Donc est le nombre minimal qui vérifie cette propriété. On l’appelle le nombre de Ramsey de et on le note .

Évidemment, en tant que mathématicien, on cherche à généraliser ce problème : A partir d’un groupe de combien de personnes on a forcément un groupe de personnes qui se connaissent toutes ou un groupe de personnes qui ne se connaissent pas du tout ? Et si on remplace par un entier naturel quelconque ? Autrement dit sommes-nous capables de calculer ?

Figurez-vous que simplement à partir de , on ne sait toujours pas aujourd’hui répondre à cette question. Surprenant non ?

On essayera de comprendre pourquoi c’est si difficile et on verra ce qu’on est quand même capable de faire dans les prochaines parties de cette série sur les nombres de Ramsey ! 🙂