Le genre de connaissance qui n’est soutenu que par des observations et qui n’est pas encore prouvé doit être soigneusement distingué de la vérité.
Leonhard Euler
Les habitants de la ville de Königsberg (aujourd’hui appelée Kaliningrad) ont toujours aimé se promener dans leur ville. Il y a notamment, au centre de celle-ci, une partie constituée de deux ilots avec sept ponts reliant les îles et la rive, comme sur le plan du 18ème siècle ci-dessous.
Ils se sont demandés s’il était possible, lors de leur promenade, de passer sur tous les ponts sans avoir à repasser sur un pont déjà traversé. Ils ont eu beau essayer de plein de façons possible, ils n’arrivaient pas à trouver un tel parcours. En 1735, un grand mathématicien, appelé Leonhard Euler, est venu répondre définitivement à cette question et sa réponse est considérée comme la naissance de la théorie des graphes.
Mais ne donnons pas toute suite sa réponse et comme à notre habitude, on se met dans la peau du chercheur. Supposons qu’un habitant de la ville de Kaliningrad (on reste au 21ème siècle nous !) vous donne un plan de sa ville comme ci-dessous et vous pose la question suivante :
❔ Peux-tu trouver un parcours de la ville qui passe par chacun des sept ponts une et une seule fois ?
✏️ A vous de jouer ! On essaye, on dessine, on réfléchit, c’est parti !
Étape 1 : Comprendre la question
Le plus naturel c’est évidemment d’essayer de trouver un tel parcours. On prend un point de départ quelconque (on peut en effet partir d’où on veut) et on tente au crayon de dessiner une promenade qui fonctionne.
Après quelques tentatives, tout comme les habitants de la ville de Königsberg, on bloque. Cela ne semble pas possible mais on n’a pas tout essayé. Une façon de montrer que c’est impossible serait d’ailleurs de lister toutes les possibilités de parcours et de constater qu’aucune n’est possible. Mais bon avant de se lancer dans un travail peut être trop long, estimons combien de parcours différents il existe.
Il y a 
points de départs : les deux rives, l’île de gauche et l’île de droite. On peut les numéroter de 
à .
Notons que vu la disposition des ponts, on a une symétrie axiale entre les deux rives. Donc partir de l’une ou l’autre des rives est identique. On peut donc en fait se concentrer seulement sur les points de départs 
et 
.
Choisissons un point de départ, disons . On voit qu’on a trois possibilités de ponts dont deux sont en fait identiques car elles nous amènent sur la même île. Ensuite si on est allé sur l’île de gauche, on a que 
possibilités : aller sur l’île ou aller sur la rive . Si par contre on est allé sur l’île de droite, on a possibilités, enfin plutôt : revenir sur la rive , aller sur l’île ou aller sur la rive (deux ponts possibles).
C’est un peu pénible mais on peut continuer ainsi le raisonnement et faire un résumé via par exemple une sorte d’arbre de possibilités.
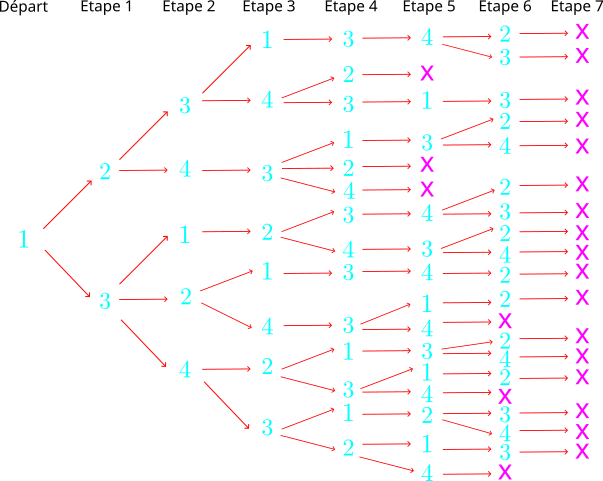
En faisant cela, on a en fait considéré toutes les possibilités en partant de et on a vu qu’elles étaient toutes impossibles. C’était déjà pénible mais on peut répéter l’opération pour le point de départ ainsi que pour le point de départ et on constatera que toutes les possibilités sont impossibles. On aura donc répondu à la question…
Pas très satisfaisant n’est-ce pas ? En tout cas cela ne l’est pas du tout pour un matheux pour notamment une raison : On n’a pas vraiment compris ce qui se passe. Si par exemple on va dans une autre ville que Königsberg, avec d’autres îles et d’autres ponts, on devra refaire un raisonnement de zéro qui pourra en plus être encore plus long s’il y a plus de ponts et plus d’îles !
Essayons donc d’y voir plus clair.
Étape 2 : Simplifier le problème
On a déjà remarqué quelques symétries qui nous ont aidé à simplifier quelques points précédemment. En dessinant les promenades sur la carte de Google, on se rend aussi compte qu’il y avait plein de détails dont on se fichait : les autres rues dans la ville, les bâtiments, la taille des ponts, etc. En fait quelles sont les seules informations importantes dans ce problème ? Les rives, les îles et comment les ponts les relient entre elles. De façon très simple, on peut donc faire un schéma avec juste des points (représentant les rives et les îles) et des lignes (représentant les ponts).
C’est fou mais je trouve qu’on y voit déjà beaucoup plus clair. En plus, je trouve cette façon de dessiner inspirante pour faire d’autres dessins plus simples et voir ce qui se passe. Par exemple avec juste deux îles :
On n’a jamais aucun problème, peu importe le nombre de ponts, on se contente de faire des aller-retours entre les deux îles ce qui est toujours possible tant qu’on n’a pas tout traversé.
Regardons avec îles maintenant. En traçant petit à petit des ponts et en regardant à chaque fois si un problème se crée ou pas, on se rend compte qu’il peut y avoir un souci avec le dessin assez simple suivant :
Il y a un problème si on prend le cercle n’ayant que deux ponts reliés à lui comme point de départ. Si on choisit un autre point de départ, on a bien une solution.
Le 
dans le dessin signifie départ et le 
signifie arrivée. On vient donc de constater que le choix du départ (et potentiellement de l’arrivée ?) a une influence sur le fait que ce soit possible ou non.
Qu’a-il de différent ce point de départ qui pose problème dans notre exemple à points ? Il a deux ponts reliés à lui alors que les autres en ont . Peut être qu’avoir seulement ponts c’est trop contraignant pour le départ ? On a besoin d’y partir, donc on utilise un pont puis il ne nous reste plus qu’un seul pont pour revenir, on sera donc obligé d’utiliser ce pont en dernier (ce sera donc aussi notre arrivée). Ah mais ! C’est intéressant cette histoire d’aller puis de repartir. Quand on y réfléchit, on fait ça avec chaque point, on arrive puis on repart, sauf potentiellement pour le départ et l’arrivée ! Pour le départ on peut ne faire que partir et pour l’arrivée on peut ne faire qu’y aller ! Mais oui c’est ça la différence avec les autres points !
Que faut-il pour être capable d’aller et de partir d’un point ? Il faut deux ponts. Dans l’exemple de Königsberg on a vu qu’on pouvait aussi revenir plusieurs fois sur une île. Mais à chaque fois si on veut y aller il faut un pont, puis pour en repartir il faut un pont supplémentaire. Il faut donc en fait un nombre pair de ponts pour chaque point qui n’est ni un point de départ ni un point d’arrivée. Si jamais ce n’est pas le cas, il n’y a aucune chance que ce soit possible.
Revenons à notre exemple de Königsberg et comptons les ponts reliés à chaque point. On indique à l’intérieur des points ce nombre de ponts.
Les points ont un nombre impair de ponts ! Cela peut potentiellement arriver pour le départ et l’arrivée donc pour points mais pas pour les ! Il est donc impossible que nous trouvions une telle promenade !
Conclusion
Le plus important dans ce problème est le fait d’avoir compris ce qui était important et ce qui ne l’était pas. Il devient beaucoup plus simple de raisonner avec juste des points et des ponts plutôt que des images détaillées de Google Maps.
Ce type de dessin avec des points et des ponts s’appelle un graphe. Les points s’appellent en fait les sommets et les ponts s’appellent les arêtes. Il y aussi un nom pour le nombre d’arêtes reliées à un sommet, on appelle cela le degré du sommet. Et enfin, s’il existe une promenade qui passe par toutes les arêtes du graphe une et seule fois, on appelle cela un chemin eulérien.
Plus précisément, on parlerai ici de multigraphe car il peut y avoir plusieurs arêtes entre deux sommets.
Suite à ce problème de Königsberg résolu par Euler, les mathématiciens se sont rendus compte que beaucoup d’autres problèmes pouvaient être interprétés via des graphes de façon plus ou moins évidentes. L’étude des graphes est donc devenu un domaine des mathématiques qui, encore aujourd’hui, est l’un des plus riches. C’est aussi l’un de mes domaines préférés et je ne manquerai pas de vous écrire plein d’autres articles sur ce sujet 🙂
Pour aller plus loin
En utilisant le vocabulaire appris lors de la conclusion, nous avons montré que :
Théorème : Dans un graphe, s’il existe strictement plus que deux sommets ayant un degré impair alors il n’existe pas de chemin eulérien pour ce graphe.
Comme souvent, quand on a un résultat de la forme « Si… Alors… » on se demande si la réciproque est aussi vraie. C’est à dire ici qu’on peut se poser la question :
❔Si un graphe n’a pas de chemin eulérien, cela signifie-t-il forcément qu’il a strictement plus que deux sommets de degré impair ?
En fait, on formulera plutôt les choses sous la forme de la contraposée (il faut avoir fait un peu de logique ici). Cette réciproque est en fait équivalente à la question :
❔ Si un graphe a moins de deux sommets de degré impair, existe-t-il forcément un chemin eulérien ?
Je laisse les intéressés réfléchir à cette question.
Énigme bonus
Je vous propose aussi une autre petite énigme sympathique, où vous pouvez utiliser ce que nous avons vu pour la résoudre :
❔ Est-il possible, sans lever le crayon, de passer par tous les côtés des rectangles une et une seule fois ? Par exemple, une tentative infructueuse est dessinée ci-dessous.
Bon courage et à la prochaine ! 🙂
