Pour des conseils généraux sur le Kangourou des Mathématiques, cliquez là.
Je vous propose ici une correction détaillée de ce sujet du Kangourou des Mathématiques 2023 destiné aux élèves de 6ème/5ème. Vous pouvez retrouver d’autres sujets ainsi que toutes les infos sur le concours sur le site officiel du Kangourou.
✏️ A vous de jouer ! Cette correction n’a aucun intérêt si vous n’avez pas essayé de faire le sujet, alors faites-le avant ! Bon courage 🙂
Questions à 3 points
Question 1

On peut obtenir directement la réponse souhaitée en faisant la soustraction ![]() ce qui est tout à fait faisable de tête (voir mon article sur le calcul mental si vous souhaitez progresser là-dessus).
ce qui est tout à fait faisable de tête (voir mon article sur le calcul mental si vous souhaitez progresser là-dessus).
Une autre façon de faire si on n’est pas à l’aise avec les soustractions c’est de regarder les possibilités de réponse et d’éliminer les plus évidentes puis de tester celles qui restent. Par exemple la réponse ![]() et la réponse
et la réponse ![]() sont clairement fausses. Ensuite on a le choix entre
sont clairement fausses. Ensuite on a le choix entre ![]() et
et ![]() . Seul le chiffre des dizaines change, on a donc juste à regarder quel dizaine convient et on se rend compte qu’il faut que ce soit
. Seul le chiffre des dizaines change, on a donc juste à regarder quel dizaine convient et on se rend compte qu’il faut que ce soit ![]() .
.
La réponse est donc ![]() .
.
Question 2

Pas le temps de réfléchir à une justification élaborée ici (on a juste à trouver la bonne réponse de toute façon). On essaye chacune des figures en espérant qu’il y en ait ![]() pour lesquelles ce soit possible de façon évidente.
pour lesquelles ce soit possible de façon évidente.
On peut séparer le triangle en deux triangles en traçant simplement la hauteur.
On peut séparer le rectangle en deux triangles en traçant une diagonale.
On peut séparer le trapèze en deux triangles en traçant une diagonale, idem pour le carré.
Il ne reste donc que l’hexagone régulier, par sécurité on essaye un peu de tracer des traits et on voit qu’a priori cela n’est pas possible ce qui nous conforte dans notre choix.
La réponse est donc ![]() Hexagone régulier.
Hexagone régulier.
Question 3

On peut ici le plus rapidement possible compléter le tableau (il reste 28 nombres à écrire) mais c’est quand même long. On va plutôt à nouveau profiter du fait que ce soit un QCM et on va essayer les réponses une par une.
En se demandant si la première pièce marche, on se demande en fait ce qu’il y a en dessous du ![]() . Pour cela on observe que pour passer de la ligne
. Pour cela on observe que pour passer de la ligne ![]() à la ligne
à la ligne ![]() , on ajoute
, on ajoute ![]() aux nombres. Donc en dessous de
aux nombres. Donc en dessous de ![]() ce sera
ce sera ![]() .
.
Cela permet aussi d’éliminer les réponses ![]() et
et ![]() .
.
Enfin pour trancher entre ![]() et
et ![]() , il faut savoir ce qui est en dessous de
, il faut savoir ce qui est en dessous de ![]() . On doit avoir en dessous
. On doit avoir en dessous ![]() .
.
La réponse est donc ![]() .
.
Question 4

A nouveau on profite que ce soit un QCM et on regarde les réponses une par une. On voit qu’elles sont classées par ordre croissant et qu’on nous demande le plus grand nombre, donc on va regarder les réponses de la ![]() à la
à la ![]() . Dès qu’on en trouve une qui marche, on peut s’arrêter car les autres réponses, même si elles marchent, seront plus petites.
. Dès qu’on en trouve une qui marche, on peut s’arrêter car les autres réponses, même si elles marchent, seront plus petites.
Pour écrire ![]() , le chiffre
, le chiffre ![]() demande déjà
demande déjà ![]() allumettes (notez que c’est indiqué par l’énoncé) donc c’est sûr qu’on va dépasser le nombre d’allumettes dont on dispose.
allumettes (notez que c’est indiqué par l’énoncé) donc c’est sûr qu’on va dépasser le nombre d’allumettes dont on dispose.
Pour écrire ![]() , le chiffre
, le chiffre ![]() demande
demande ![]() allumettes et chaque
allumettes et chaque ![]() demande
demande ![]() allumettes. On a donc besoin de
allumettes. On a donc besoin de ![]() allumettes. C’est bon ça marche, on peut donc s’arrêter là !
allumettes. C’est bon ça marche, on peut donc s’arrêter là !
La réponse est donc ![]() .
.
Question 5

Ici bien comprendre l’énoncé demande sans doute une relecture. Il faut bien noter qu’elle a ![]() disques mais elle construit des tours de
disques mais elle construit des tours de ![]() disques. Pas vraiment d’autres choix que de compter en faisant attention de ne rien oublier.
disques. Pas vraiment d’autres choix que de compter en faisant attention de ne rien oublier.
On numérote les disques de ![]() à
à ![]() avec
avec ![]() correspondant au disque le plus petit et
correspondant au disque le plus petit et ![]() au disque le plus grand. Pour la base de notre tour, on ne peut commencer qu’avec le disque
au disque le plus grand. Pour la base de notre tour, on ne peut commencer qu’avec le disque ![]() ou
ou ![]() (sinon impossible de mettre
(sinon impossible de mettre ![]() autres disques ensuite).
autres disques ensuite).
Si on commence avec ![]() , la seule possibilité est ensuite
, la seule possibilité est ensuite ![]() .
.
Si on commence avec ![]() , on a
, on a ![]() possibilités ensuite :
possibilités ensuite : ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
La réponse est donc ![]() .
.
Question 6

On profite à nouveau du fait que ce soit un QCM et on teste les réponses une par une.
Pour que la première ait une chance de marcher, il faut placer le ![]() dans le « cercle isolé » car
dans le « cercle isolé » car ![]() et
et ![]() sont plus proches l’un de l’autre. On voit qu’en tournant la roue de
sont plus proches l’un de l’autre. On voit qu’en tournant la roue de ![]() unité par rapport à l’exemple de l’énoncé cela marche ! On peut donc directement s’arrêter là.
unité par rapport à l’exemple de l’énoncé cela marche ! On peut donc directement s’arrêter là.
La réponse est donc ![]() et
et ![]() .
.
Question 7

Ici il s’agit de bien comprendre quel ruban est le plus en dessous (et a donc forcément été mis en premier). On voit que ![]() est un bon candidat vu qu’il est en dessous de
est un bon candidat vu qu’il est en dessous de ![]() et
et ![]() . De plus
. De plus ![]() est au dessus de
est au dessus de ![]() et
et ![]() donc on est sûr que
donc on est sûr que ![]() a été mis en premier.
a été mis en premier.
On sait aussi du coup que ![]() a été mis en dernier et il nous reste à savoir l’ordre entre
a été mis en dernier et il nous reste à savoir l’ordre entre ![]() et
et ![]() . Pour cela c’est la petite face carré de devant qui nous indique que
. Pour cela c’est la petite face carré de devant qui nous indique que ![]() est en dessous de
est en dessous de ![]() .
.
Finalement la réponse est donc ![]() .
.
Question 8

Pas vraiment de raisonnement particulier ici, il s’agit surtout de vision géométrique. On peut néanmoins s’aider des points en arrière-plan pour être sûr que tout fonctionne bien. Ici on voit que ![]() et
et ![]() s’emboîtent parfaitement et forment bien un hexagone.
s’emboîtent parfaitement et forment bien un hexagone.
La réponse est donc ![]() et
et ![]() .
.
Questions à 4 points
Question 9

Ici il s’agit de traduire l’énoncé français en un énoncé mathématique, c’est assez typique des exercices « classiques » de collège sur la résolution des équations à une inconnue.
On note ![]() le nombre de maisons où habitent
le nombre de maisons où habitent ![]() personnes. On cherche
personnes. On cherche ![]() et on sait qu’on a l’équation suivante :
et on sait qu’on a l’équation suivante :
![]()
Le ![]() est le nombre de maisons habitées par
est le nombre de maisons habitées par ![]() personnes. On résout cette équation :
personnes. On résout cette équation :
![]()
La réponse est donc ![]() .
.
Question 10

Il s’agit à nouveau de trouver un nombre inconnu, ici une largeur qu’on va noter ![]() . On donne aussi des noms au côté du carré
. On donne aussi des noms au côté du carré ![]() et à la longueur du rectangle
et à la longueur du rectangle ![]() (qui est aussi la longueur d’un côté du triangle). Notons
(qui est aussi la longueur d’un côté du triangle). Notons ![]() le périmètre d’une figure (il est le même pour chaque figure d’après l’énoncé). On écrit alors les informations qu’on possède :
le périmètre d’une figure (il est le même pour chaque figure d’après l’énoncé). On écrit alors les informations qu’on possède :
![]()
![]()
![]()
Ici on a ![]() , la troisième équation nous permet donc d’en déduire que
, la troisième équation nous permet donc d’en déduire que ![]() . Puis en utilisant la première équation on déduit que
. Puis en utilisant la première équation on déduit que ![]() .
.
Enfin on utilise la deuxième équation pour trouver ![]() :
:
![]()
La réponse est donc ![]() .
.
Question 11

Le mieux ici est d’écrire chaque terme en puissance de ![]() . On a
. On a
![]()
Le résultat de la multiplication est donc :
![]()
Il faut donc enlever le terme ![]() pour obtenir
pour obtenir ![]() .
.
La réponse est ![]() .
.
Question 12

L’énoncé sous-entend qu’on devrait pouvoir réussir à compléter les cases d’une seule façon. Si on regarde les deux premières cases, on voit que leur produit doit faire ![]() et cela nous donne beaucoup de possibilités :
et cela nous donne beaucoup de possibilités : ![]() et
et ![]() ,
, ![]() et
et ![]() ,
, ![]() et
et ![]() ,
, ![]() et
et ![]() (ainsi que le fait qu’on ne sache pas qui est dans la première case et qui est dans la deuxième). C’est une épreuve de vitesse et à partir du moment où on a trouvé un moyen de résoudre le problème, on y va (sauf si c’est vraiment trop long).
(ainsi que le fait qu’on ne sache pas qui est dans la première case et qui est dans la deuxième). C’est une épreuve de vitesse et à partir du moment où on a trouvé un moyen de résoudre le problème, on y va (sauf si c’est vraiment trop long).
Néanmoins, encore une fois on sait qu’il n’y a qu’une bonne réponse (c’est la règle de ce QCM), donc on va commencer par essayer une possibilité qui nous parait bien. Personnellement je trouve que ![]() et
et ![]() ou
ou ![]() et
et ![]() sont trop extrêmes. La première plausible est
sont trop extrêmes. La première plausible est ![]() et
et ![]() mais le
mais le ![]() ne peut pas être dans la deuxième case car ce n’est pas possible d’obtenir
ne peut pas être dans la deuxième case car ce n’est pas possible d’obtenir ![]() ensuite avec, donc mettons
ensuite avec, donc mettons ![]() puis
puis ![]() .
.
A partir de là on n’a plus le choix. Ensuite c’est ![]() . Mais
. Mais ![]() ne peut pas permettre d’obtenir
ne peut pas permettre d’obtenir ![]() donc notre remplissage n’était pas bon.
donc notre remplissage n’était pas bon.
Mettons donc plutôt ![]() et
et ![]() dans deux premières cases, sachant qu’on doit commencer avec
dans deux premières cases, sachant qu’on doit commencer avec ![]() car sinon on ne pourra pas obtenir
car sinon on ne pourra pas obtenir ![]() . On a donc
. On a donc ![]() puis ensuite c’est
puis ensuite c’est ![]() , duquel on déduit
, duquel on déduit ![]() et pour finir
et pour finir ![]() . Cela marche, plus qu’à faire la somme. On a
. Cela marche, plus qu’à faire la somme. On a
![]()
La réponse est donc ![]() .
.
Question 13

Bon ici il est beaucoup mieux de savoir immédiatement qu’un an correspond à ![]() semaines.
semaines.
Si jamais on ne le sait pas, on peut toujours s’en sortir en sachant qu’un an c’est ![]() jours et qu’une semaine c’est
jours et qu’une semaine c’est ![]() jours, et de voir que
jours, et de voir que ![]() donc un an est environ
donc un an est environ ![]() semaines.
semaines.
Il faut donc calculer ![]() divisé par
divisé par ![]() . On ne cherche heureusement pas à avoir un résultat exact mais simplement une approximation suffisante pour répondre à la question. On voit que
. On ne cherche heureusement pas à avoir un résultat exact mais simplement une approximation suffisante pour répondre à la question. On voit que ![]() (je vous invite à nouveau à consulter mon article sur le calcul mental si vous souhaitez progresser là-dessus). On peut continuer,
(je vous invite à nouveau à consulter mon article sur le calcul mental si vous souhaitez progresser là-dessus). On peut continuer, ![]() . C’est rassurant, car on est très proche des
. C’est rassurant, car on est très proche des ![]() semaines et on nous dit que son anniversaire arrive bientôt. C’est quand même un peu perturbant car d’après notre calcul elle a
semaines et on nous dit que son anniversaire arrive bientôt. C’est quand même un peu perturbant car d’après notre calcul elle a ![]() ans et
ans et ![]() semaine donc son anniversaire vient de passer mais en vérifiant une fois notre calcul, on se dit que c’est sans doute dû au fait qu’un an n’est pas pile
semaine donc son anniversaire vient de passer mais en vérifiant une fois notre calcul, on se dit que c’est sans doute dû au fait qu’un an n’est pas pile ![]() semaines mais un peu plus.
semaines mais un peu plus.
La réponse est donc ![]() ans.
ans.
Question 14

Si vous avez lu mon article sur les ponts de Königsberg, cette question peut être vue avec des graphes. Mais ici je pars évidemment du principe qu’on ne sait pas ça.
Tout comme dans une des questions précédentes (la question ![]() ), il va falloir bien compter en faisant attention de ne rien oublier. Pour cela, on peut remarquer que le rectangle du milieu est adjacent à tous les autres rectangles. Autrement dit une fois sa couleur choisie, il faudra colorier les autres rectangles avec seulement
), il va falloir bien compter en faisant attention de ne rien oublier. Pour cela, on peut remarquer que le rectangle du milieu est adjacent à tous les autres rectangles. Autrement dit une fois sa couleur choisie, il faudra colorier les autres rectangles avec seulement ![]() couleurs. On a
couleurs. On a ![]() possibilités pour la couleur de ce rectangle du milieu.
possibilités pour la couleur de ce rectangle du milieu.
Ensuite une fois choisie la couleur d’un autre rectangle, le coloriage nous est en fait imposé : On doit avoir une alternance de couleurs entre les autres rectangles. On a donc juste ![]() possibilités venant de cette couleur à choisir.
possibilités venant de cette couleur à choisir.
Ainsi au total on a
![]()
La réponse est donc ![]() .
.
Question 15

Il faut ici trouver le nombre de trois chiffres différents le plus grand et aussi trouver le plus petit.
Le chiffre des centaines doit être le plus grand possible : ![]() . Ensuite pour le chiffre des dizaines on ne peut plus prendre
. Ensuite pour le chiffre des dizaines on ne peut plus prendre ![]() donc on prend
donc on prend ![]() . Et enfin pour les unités on ne peut plus prendre
. Et enfin pour les unités on ne peut plus prendre ![]() et
et ![]() donc on prend
donc on prend ![]() . Le nombre à
. Le nombre à ![]() chiffres différents le plus grand est donc
chiffres différents le plus grand est donc ![]() .
.
On fait un raisonnement similaire pour trouver le nombre le plus petit, en faisant un peu attention. On prend ![]() pour le chiffre des centaines. Ensuite on a le droit au
pour le chiffre des centaines. Ensuite on a le droit au ![]() pour les dizaines alors qu’on ne pouvait pas le prendre pour les centaines. Puis on finit par le
pour les dizaines alors qu’on ne pouvait pas le prendre pour les centaines. Puis on finit par le ![]() . Le nombre à
. Le nombre à ![]() chiffres différents le plus petit est donc
chiffres différents le plus petit est donc ![]() .
.
Enfin il faut réussir à faire la différence
![]()
La réponse est donc ![]() .
.
Question 16

Ce qu’on remarque d’important c’est que le chiffre des dizaine change entre le premier et le deuxième nombre. Vu qu’ils sont consécutif, cela nous dit déjà que le triangle ▲ est forcément un ![]() , la croix ✖ est un
, la croix ✖ est un ![]() et donc le carré ■ est un
et donc le carré ■ est un ![]() . Or le carré ■ intervient aussi comme chiffre des dizaines du premier nombre. On en déduit donc que le premier nombre est
. Or le carré ■ intervient aussi comme chiffre des dizaines du premier nombre. On en déduit donc que le premier nombre est ![]() . Les deux nombres suivants sont donc
. Les deux nombres suivants sont donc ![]() et
et ![]() et le cœur ♥ est un
et le cœur ♥ est un ![]() . Il faut donc écrire
. Il faut donc écrire ![]() en symboles.
en symboles.
La réponse est donc ![]() .
.
Questions à 5 points
Question 17

La première chose à faire est de déterminer le nombre de figures qu’il y a dans cette case en bas au milieu. Notons ![]() ce nombre qu’on cherche.
ce nombre qu’on cherche.
La case de gauche au milieu a alors ![]() figures. Celle de droite au milieu en a
figures. Celle de droite au milieu en a ![]() . Donc en se servant de la case du haut on déduit qu’on a
. Donc en se servant de la case du haut on déduit qu’on a
![]()
Donc
![]()
Cela nous permet déjà d’éliminer les réponses ![]() .
.
Enfin, pour qu’il y ait bien ![]() cercles et
cercles et ![]() triangles à la fin, on se rend compte qu’il faut mettre un triangle et un cercle dans la case.
triangles à la fin, on se rend compte qu’il faut mettre un triangle et un cercle dans la case.
La réponse est donc ![]() .
.
Question 18
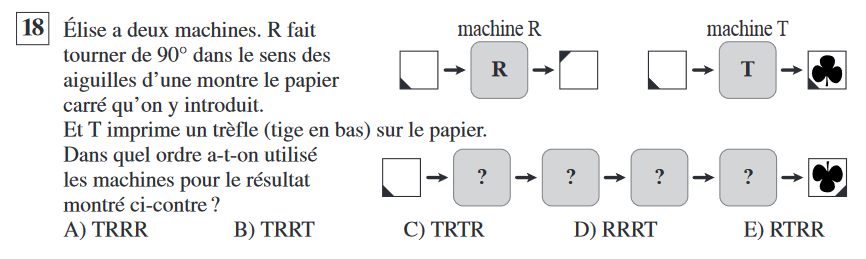
On voit qu’on a tourné ![]() fois de
fois de ![]() dans le sens des aiguilles d’une montre et qu’on a imprimé un trèfle. Il s’agit donc juste de déterminer à quel moment on a imprimé le trèfle. Pour cela il faut savoir combien de fois le trèfle a tourné. On voit qu’il a tourné
dans le sens des aiguilles d’une montre et qu’on a imprimé un trèfle. Il s’agit donc juste de déterminer à quel moment on a imprimé le trèfle. Pour cela il faut savoir combien de fois le trèfle a tourné. On voit qu’il a tourné ![]() fois de
fois de ![]() . Ainsi il faut exactement deux opération de rotations après impression du trèfle.
. Ainsi il faut exactement deux opération de rotations après impression du trèfle.
La réponse est donc ![]() .
.
Question 19

Pas le temps de réfléchir plus que ça ici, on teste toutes les possibilités. Je note R pour recto et V pour verso. La notation RRV signifie « 1ère carte recto, 2ème carte recto et 3ème carte verso ».
- RRR :
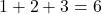
- RRV :
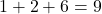
- RVR :
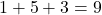
- RVV :
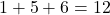
- VRR :
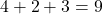
- VRV :
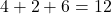
- VVR :
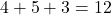
- VVV :
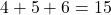
On a donc ![]() possibilités de sommes différentes.
possibilités de sommes différentes.
La réponse est ![]() .
.
Question 20

Ici on voit qu’on a un quadrillage pour nous aider à « calculer » les aires. Disons qu’un carré du quadrillage est d’aire ![]() et calculons l’aire de chaque figure à partir de cette référence.
et calculons l’aire de chaque figure à partir de cette référence.
Chacun des ![]() carrés remplis partiellement par la figure A est rempli de moitié. On en déduit que l’aire de A est
carrés remplis partiellement par la figure A est rempli de moitié. On en déduit que l’aire de A est ![]() .
.
Idem pour la figure B.
La figure C est un peu plus compliquée, on regarde donc rapidement la D avant. De la même façon que pour la A, la figure D remplit aussi chaque carré à moitié donc même aire que A et B.
Enfin il faut regarder la C, soit son aire va être plus grande, soit elle va être la même que les autres d’après les possibilités de réponse. Cette fois-ci c’est difficile de savoir en regardant carré par carré ce qu’elle remplit. Dans les carrés du haut elle remplit moins que la moitié mais dans les carrés du bas elle remplit davantage, mais on ne sait pas si la compensation fait qu’on a une aire identique au final.
Pour trancher, il faut se rendre compte que la figure C, regardée de gauche à droite, forme un début de triangle sur la moitié de la longueur mais par contre en hauteur elle ne descend pas complètement. Si jamais elle descendait complètement, on aurait un triangle qui correspondrait à la moitié du rectangle composé de deux carrés. Et donc la figure C serait en fait 4 triangles dont chacun est une moitié de rectangle constitué de deux carrés et finalement la figure C remplirait 2 carrés donc aurait la même aire que les autres figures.
Mais vu qu’elle ne descend pas complètement, cela signifie qu’on a une partie qui occupe plus d’espace et donc l’aire est un peu plus grande que l’explication précédente.
Finalement, la réponse est donc ![]() .
.
Question 21

C’est assez difficile de donner des conseils ici car il s’agit de vision dans l’espace. Il faut trouver une façon de plier le patron de façon à obtenir les deux sommets sur une même face (il y a en effet des façons de le plier telles que ce ne soit pas le cas).
Ici en considérant B comme la face du bas et en pliant O et R par dessus (R étant donc la face du haut). Puis en enroulant V,N et J sur les côtés du cube, on se rend compte que les points sont communs à la face noire.
La réponse est donc ![]() .
.
Question 22

Il faut bien connaître comment on fait une multiplication en la posant. On commence par faire ![]() et cela nous permet d’écrire un
et cela nous permet d’écrire un ![]() . Cela signifie qu’il y a eu une retenue, il faut trouver laquelle. En répétant sa table de
. Cela signifie qu’il y a eu une retenue, il faut trouver laquelle. En répétant sa table de ![]() dans sa tête, on se rend compte qu’il y a seulement
dans sa tête, on se rend compte qu’il y a seulement ![]() qui permet d’obtenir un nombre terminant par un
qui permet d’obtenir un nombre terminant par un ![]() . Le
. Le ![]() est donc un
est donc un ![]() et on a retenu
et on a retenu ![]() .
.
On continue le raisonnement : on fait ensuite ![]() et cela nous permet d’écrire un
et cela nous permet d’écrire un ![]() . N’oublions pas qu’on avait une retenue de
. N’oublions pas qu’on avait une retenue de ![]() . On avait donc un
. On avait donc un ![]() auquel on a ajouté
auquel on a ajouté ![]() . En répétant à nouveau notre table de
. En répétant à nouveau notre table de ![]() , on voit que
, on voit que ![]() convient donc
convient donc ![]() et on a retenu
et on a retenu ![]() .
.
On continue jusqu’à ce qu’on trouve la lettre qui représente un ![]() . On a
. On a ![]() et on a écrit
et on a écrit ![]() avec une retenue de
avec une retenue de ![]() . On avait donc un
. On avait donc un ![]() auquel on a ajouté
auquel on a ajouté ![]() . La seule opération qui convient est donc
. La seule opération qui convient est donc ![]() . Donc
. Donc ![]() et on peut s’arrêter là vu qu’on a trouvé notre réponse !
et on peut s’arrêter là vu qu’on a trouvé notre réponse !
La réponse est ![]() .
.
Question 23

On teste toutes les possibilités.
- Si Maya dit la vérité alors tous les autres doivent mentir. Le coupable est Paul vu que Maya dit la vérité. Paul ment en disant que c’est Rose. Mais Rose et Tom disent la vérité en disant que ce n’est pas eux. Cela ne convient pas.
- Si Paul dit la vérité. Le coupable est alors Rose. Maya ment en disant que c’est Paul. Rose ment en disant que ce n’est pas elle. Mais Tom dit la vérité en disant que ce n’est pas lui. Cela ne convient pas.
- Si Rose dit la vérité. Tous les autres doivent mentir, en particulier vu que Tom doit mentir, cela signifie que c’est lui le coupable. Maya dit que c’est Paul donc elle ment. Paul dit que c’est Rose donc il ment. Tout cela est cohérent. Mais attention ! Il faut quand même vérifier la dernière possibilité car dans les choix de réponses il y a le fait qu’il est impossible de savoir, ce qui peut arriver si deux possibilités sont possibles.
- Si Tom dit la vérité. Tous les autres voient mentir, en particulier Rose doit mentir, cela signifie que c’est elle la coupable. Mais alors Paul dit la vérité en disant que c’est Rose la coupable, ce n’est pas cohérent.
La seule possibilité est donc que Rose dise la vérité et c’est alors Tom le coupable.
La réponse est donc ![]() .
.
Question 24

On peut rapidement compléter la tour et ainsi avoir facilement la réponse mais évidemment on manque peut être de temps pour faire cela. En complétant quand même un peu la tour on se rend compte d’un pattern : On place à chaque fois un nombre pair avec en dessous de lui l’impair inférieur.
Vu que toutes les réponses sont dans la zone autour de ![]() on peut dessiner seulement cette portion de la tour plutôt que toute la tour.
on peut dessiner seulement cette portion de la tour plutôt que toute la tour.
De haut en bas on a ![]() .
.
On voit alors que seuls ![]() et
et ![]() , parmi les choix de réponses, sont collés.
, parmi les choix de réponses, sont collés.
La réponse est donc ![]() .
.
Questions Bonus
Question 25

Les nombres sont très grand mais on nous demande juste le chiffre des milliers. On pose donc la multiplication jusqu’à obtenir la réponse.

La réponse est donc ![]() .
.
Question 26

Déjà, il y aura forcément ![]() dans la date donc on a déjà la somme
dans la date donc on a déjà la somme ![]() . Il reste
. Il reste ![]() à obtenir avec le jour et le mois. On sait aussi que le mois est un nombre compris entre
à obtenir avec le jour et le mois. On sait aussi que le mois est un nombre compris entre ![]() et
et ![]() tandis que le jour est compris entre
tandis que le jour est compris entre ![]() et
et ![]() (il faudra peut être faire attention aux mois qui contiennent bien
(il faudra peut être faire attention aux mois qui contiennent bien ![]() ).
).
On sent que ![]() c’est un nombre assez grand à obtenir avec ces contraintes. Soyons un peu plus précis. La somme maximale que peut donner un mois est
c’est un nombre assez grand à obtenir avec ces contraintes. Soyons un peu plus précis. La somme maximale que peut donner un mois est ![]() (avec
(avec ![]() ). La somme maximale que peux donner un jour est
). La somme maximale que peux donner un jour est ![]() (avec
(avec ![]() ). Avec cela en tête, on va liste les possibilités :
). Avec cela en tête, on va liste les possibilités :
- Si la valeur du mois est
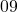 . Il faut alors qu’on est
. Il faut alors qu’on est 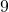 en somme pour les jours. C’est possible avec
en somme pour les jours. C’est possible avec 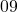 ,
, 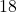 et
et 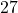 .
. - Si la valeur du mois est
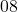 . Il faut alors qu’on est
. Il faut alors qu’on est 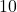 en somme pour les jours. C’est possible avec
en somme pour les jours. C’est possible avec 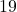 et
et 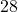 .
. - Si la valeur du mois est
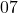 il faut alors qu’on est
il faut alors qu’on est  en somme pour les jours. C’est possible avec
en somme pour les jours. C’est possible avec 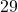 uniquement.
uniquement. - Si la valeur du mois est
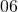 , il faut alors qu’on est
, il faut alors qu’on est 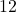 en somme pour les jours mais on a remarqué précédemment que c’est impossible.
en somme pour les jours mais on a remarqué précédemment que c’est impossible. - C’est aussi impossible pour toutes les autres valeurs de mois étant donné qu’on aura toujours une somme du mois
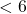 et donc une somme trop élevée à faire avec le jour.
et donc une somme trop élevée à faire avec le jour.
Finalement les dates possibles sont ![]() et
et ![]() .
.
La réponse est donc ![]() .
.
Remarques et conclusion
Même si ce n’est pas particulièrement difficile, il est facile de se tromper lorsqu’il faut compter les possibilités (questions 5,14,19).
Il y aussi des questions piégeuses dans ce sujet, je pense notamment à la question 20. La question 15 demande aussi de ne pas oublier que ![]() est une possibilité pour les dizaine/unités.
est une possibilité pour les dizaine/unités.



Une autre façon d’expliquer :
Question 25 :
Pour avoir le chiffre des dizaines, il suffit de faire le produit des deux derniers nombres des deux chiffres .
Pour avoir le chiffre des centaines, le produit des trois derniers.
Pour avoir le chiffre des milliers, le produit des quatre derniers des deux chiffres : 6789×4321.
Réponse : le chiffre des milliers est 5