Comprendre et comprendre

Je crois que voilà un des principes fondamentaux de la réalité : accepter que les choses difficiles à comprendre soient difficiles à comprendre.

Haruki Murakami

Bien que classé piste grise, cet article discute de que veut dire comprendre en se basant sur un exemple d’une propriété mathématique. L’énoncé de l’exemple s’apprend au lycée mais quelques aspects (définition d’une fonction continue, d’une intégrale, etc) sont plutôt accessibles pour les licences/prépas. Néanmoins il est possible de suivre une partie de la discussion sans avoir toutes ces connaissances.

Quand pouvons-nous dire que nous avons compris quelque chose ? On ne peut pas répondre à cette question précisément car derrière le mot « comprendre » se cache en fait plusieurs significations. J’aimerais parler ici d’un des points les plus importants des mathématiques selon moi : ce qu’est un « niveau de compréhension suffisant ».

Je vais chercher à être assez concret bien que le concept soit plutôt vague. Pour cela, rien de mieux que de prendre l’exemple d’une propriété et d’expliquer les différents niveaux de compréhension qu’on peut avoir à propos de celle-ci. Voici donc l’exemple que je propose :

Théorème : Soit a\leq b des réels et soit f:[a,b]\rightarrow \mathbb{R} une fonction continue. Soit F une primitive de f. Alors

    \[\int_{a}^{b}f(t)dt=F(b)-F(a)\]

La compréhension ligne par ligne

Il s’agit de comprendre la définition de chaque mot d’une phrase.

Par exemple ici, je comprends que :

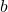  • a et b sont des réels, ils peuvent valoir 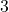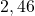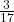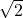3, 2,46, \frac{3}{17}, \sqrt{2},etc.
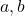  • [a,b] signifie le segment a,b, c’est à dire tous les réels compris entre a et b.
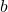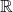  • \mathbb{R} est l’ensemble des réels.
  • Je connais la définition d’une fonction continue :

        \[\forall x_0\in [a,b] \forall \epsilon >0 \exists \eta>0 \text{ tels que } \forall x\in [x_0-\eta,x_0+\eta] \text{ on a } |f(x)-f(x_0)|\leq \epsilon.\]

  • Je sais ce qu’est une primitive, cela veut dire que la dérivée de 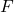F est égale à f.
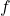  • Je sais ce que veut dire 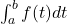\int_{a}^{b}f(t)dt, c’est l’intégrale de 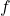f sur [a,b] et je connais la définition de l’intégrale issue de mon cours.

Cette compréhension est le minimum que l’on cherche à avoir lorsqu’on prend des notes. On essaye souvent de comprendre un peu plus loin mais disons que dans le pire des cas on veut être sûr de comprendre au moins les mots qu’on écrit. S’il y a un mot qu’on ne comprend pas, il faut absolument poser la question !

La compréhension pratique

Il s’agit de comprendre à quoi va nous servir une propriété et comment s’en servir.

Par exemple ici, je comprends que ce théorème va m’aider à calculer des intégrales. Si on me donne une intégrale à calculer telle que

    \[\int_{0}^{1}xdx\]

alors je vais chercher une primitive de la fonction intégrée, ici la fonction F:x\in [0,1]\rightarrow\frac{1}{2}x^2\in \mathbb{R} convient. Ensuite je me sers du théorème pour dire que

    \[\int_{0}^{1}xdx = F(1)-F(0)=\frac{1}{2}1^2-\frac{1}{2}0^2=\frac{1}{2}\]

La compréhension intuitive

Il s’agit d’être capable d’expliquer avec des mots simples (et de façon imagée si possible) ce que dit la propriété.

Par exemple ici :

  • Comprendre intuitivement ce qu’est une fonction continue, c’est-à-dire une fonction qu’on peut tracer sans lever son crayon.
  • Comprendre intuitivement ce que représente une intégrale, c’est-à-dire l’aire sous la courbe de la fonction qu’on intègre.

On est capable par exemple de reprendre l’intégrale de la section précédente et de la voir visuellement.

Plus dur, mais pour que la compréhension intuitive soit complète, il faudrait rajouter le fait qu’on comprenne intuitivement ce que représente la différence des deux valeurs d’une primitive et son lien avec l’intégrale. Pour cela, vu qu’on cherche une intuition, il peut être bon de se rattacher à une situation où on comprend mieux le lien entre une fonction et sa primitive. En ayant fait un peu de physique, je pense par exemple à la vitesse et à la position (la vitesse étant la dérivée par rapport au temps de la position). Si nous connaissons la vitesse à chaque instant, il est logique qu’on soit capable de connaître quelle distance on a parcouru (correspondant à la différence entre la position d’arrivée et la position de départ). Je reste exprès un peu vague ici pour que vous puissiez vous faire votre propre compréhension du résultat.

La compréhension de pourquoi c’est vrai via une preuve

Il s’agit de comprendre pourquoi le résultat est vrai grâce à une preuve qu’on a en tête (ou qu’on est capable de trouver).

Ici, ce théorème repose sur le fait qu’il y a un lien entre primitive et intégrale. En fait, il s’agit même de montrer que la « fonction intégrale » de f est une primitive de f. Plus précisément, pour x\in[a,b] on définit la fonction G sur [a,b] par

    \[G(x)= \int_{a}^x f(t)dt\]

Je ne vais pas faire la preuve ici (ce n’est pas le but de l’article), mais si vous arrivez à montrer que cette fonction G est dérivable et de dérivée égale à f alors vous avez gagné. En effet, on sait (ou on montre) que deux primitives sont égales à une constante près. Soit F une primitive de f. On aura donc

    \[G(b)=F(b)+c\]

avec c une constante. Mais on a aussi G(a)=0=F(a)+c donc c=-F(a). D’où finalement

    \[\int_{a}^{b}f(t)dt=G(b)=F(b)-F(a).\]

A noter que comprendre cette preuve donne aussi plusieurs réponses pour la section de compréhension suivante, d’où l’intérêt de connaître et comprendre aussi une preuve.

La compréhension avancée obtenue par les questions

Il s’agit ici de s’être posé beaucoup de questions autour du sujet et d’être capable de répondre à certaines d’entre elles. Plus on a répondu à des questions, plus notre compréhension avance, sans qu’il n’y ait vraiment de limites.

Je propose ici une liste de questions :

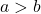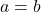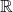  • Que se passe-t-il si a>b ? Et si a=b ? Si on n’est pas sur un segment [a,b] mais sur plusieurs segments disjoints ? Et si on est sur un ensemble de \mathbb{R} plus bizarre qu’un segment ? Est-ce que ça a du sens si 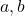a,b sont des complexes ?
  • Que se passe-t-il si la fonction 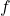f est seulement continue par morceaux ? Et si elle n’est pas continue ? Si elle est à valeurs complexes ?
  • Est-on sûr que la fonction ait une primitive ? Y-a-t-il une condition nécessaire et suffisante pour qu’une fonction ait une primitive ? Au fait, une fonction a plusieurs primitives, laquelle choisit-on ici ?
  • Pourquoi le calcul d’une intégrale est liée aux primitives ? On intègre sur tout le segment 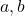a,b et finalement on n’a que 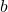b et a qui interviennent du côté droit, est-ce logique ? Pouvait-on le deviner ?
  • Je connais plusieurs définitions de l’intégrale, cette propriété est-elle vrai pour toutes les définitions que je connais ? Si oui, qu’en est-il des preuves, sont-elles identiques ?
  • Si ma fonction est positive, je sais que son intégrale est positive, le voit-on ici ? Idem pour négative. Est-ce que d’autres propriétés que je connais sur l’intégrale sont bien cohérentes avec ce résultat ?

Le but de cet article n’étant pas de comprendre particulièrement ce résultat mais simplement de comprendre ce que veut dire comprendre, je n’essaierai donc pas de répondre à toutes ces questions ici ^^

Conclusion

Lorsque vous suivez un cours, le minimum que vous devez vous assurer d’avoir au moment où vous écrivez sur votre feuille c’est la compréhension ligne par ligne. Si ce n’est pas le cas, je vous encourage à poser une question à votre enseignant ou au moins à bien noter pour vous-mêmes que ce mot là vous ne l’avez pas compris et qu’il faudra absolument l’éclaircir plus tard.

Ensuite, il est important d’acquérir à la fois une compréhension intuitive et pratique des résultats si on veut réussir à faire des exercices (ces derniers nous aident d’ailleurs à acquérir ces compréhensions). La compréhension de pourquoi c’est vrai via une preuve est selon moi agréable à avoir et peut devenir importante pour certains résultats sachant qu’une preuve comporte souvent des idées clés dont on peut se resservir.

Enfin, si on est intéressé et qu’on souhaite vraiment progresser, je ne peux que conseiller de se poser des questions. Il s’agit sans aucun doute du meilleur moyen pour progresser et j’y dédie d’ailleurs tout un article. N’oubliez pas que l’important est de vous poser vos propres questions car ce sont celles-ci qui sont adaptées à vous et vous font le plus progresser.

J’espère que cet article un peu spécial vous aidera dans votre aventure mathématique 🙂

Licences des images utilisées

Image de couverture : Image de storyset sur Freepik
Image de la main qui écrit : Image by storyset on Freepik
Image de l’ouvrier : Image by Freepik
Image des gens qui s’interrogent : Image de storyset sur Freepik

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Publications similaires