Un des avantages de la géométrie réside dans le fait que les sens peuvent venir aider la pensée à trouver le chemin à suivre.
Henri Poincaré

J’ai un faible pour les problèmes dont l’énoncé est facilement compréhensible par tous mais qui ne sont pourtant pas évidents à résoudre. Je vous présente ici l’un de mes préférés qui a en plus l’avantage d’être très visuel. Le problème est le suivant :
❔ L’objectif est de colorier le plan (imaginez une feuille blanche infinie) en respectant la contrainte suivante : lorsque deux points sont à distance ![]() l’un de l’autre, ils doivent être de couleur différente. De combien de couleurs au minimum avons-nous besoin pour colorier le plan de cette façon ?
l’un de l’autre, ils doivent être de couleur différente. De combien de couleurs au minimum avons-nous besoin pour colorier le plan de cette façon ?

✏️ A vous de jouer ! Prenez une feuille de papier et réfléchissez à cette question. Si vous n’arrivez pas à trouver la valeur exacte, essayez déjà de trouver un encadrement.
Étape 1 : Comprendre la question
Ici, comme souvent, pour bien comprendre il faut commencer par dessiner. Munissons nous d’un petit bâton de ![]() de long pour pouvoir voir quand deux points doivent être de couleur différentes.
de long pour pouvoir voir quand deux points doivent être de couleur différentes.

Notons déjà qu’il est clair que si on colorie le plan d’une seule couleur, nous n’allons pas respecter la contrainte. Il faut donc au moins deux couleurs. Avec deux couleurs, on s’ouvre déjà une multitude de façons de colorier. On peut par exemple simplement séparer le plan en deux :

Mais on voit alors qu’on a encore des problèmes un peu partout (notre superbe bâton devient rouge pour signaler un problème et vert pour dire que c’est bon). Peut-être pouvons nous colorier de façon plus astucieuse ? Enfin on sent quand même que deux couleurs ce n’est pas beaucoup et il en faudra sûrement plus.
Reprenons. Déjà je vais forcément commencer par donner une couleur, disons bleue, à un point quelque part (notons d’ailleurs que pour des raisons de symétrie, peu importe quel premier point on choisit, le problème est le même). Ensuite tous les autres points situés à ![]() de distance autour de lui devront avoir une couleur différente. Quels sont ces points ? Il s’agit des points situés sur le cercle de rayon
de distance autour de lui devront avoir une couleur différente. Quels sont ces points ? Il s’agit des points situés sur le cercle de rayon ![]() et de centre le point bleu.
et de centre le point bleu.

Est-ce que je peux colorier tous les points à l’intérieur du cercle de la même couleur ? En bougeant mon bâton je vois que ce n’est pas possible, il faudrait un cercle plus petit, plus précisément avec un cercle de diamètre ![]() cela devient possible. On va même prendre ce diamètre égal à
cela devient possible. On va même prendre ce diamètre égal à ![]() pour éviter d’avoir un problème en mettant le bâton d’une extrémité à l’autre du cercle.
pour éviter d’avoir un problème en mettant le bâton d’une extrémité à l’autre du cercle.

Que faisons-nous de l’extérieur du cercle maintenant ? Vu qu’on doit au final colorier tout le plan, ce serait bien d’avoir un motif qu’on répète à l’infini. Vu qu’on a commencé par faire un cercle, on peut imaginer répéter ce cercle. Regardons déjà deux cercles de diamètre ![]() .
.
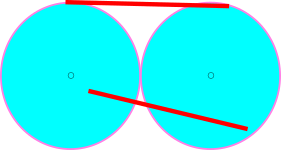
On voit que les deux intérieurs de cercle doivent être de couleurs différentes. Mmm… Il y a potentiellement aussi des problèmes avec les contours des cercles… Cela commence à être compliqué… Plutôt que de considérer les intérieurs des cercles qui nous conduisent à devoir faire attention à une infinité de points, restons sur l’idée basique que lorsqu’on a un point, le cercle de rayon ![]() centré autour de lui doit être de couleur différente. On peut reproduire ce raisonnement avec un cercle centré sur l’un des points de la bordure :
centré autour de lui doit être de couleur différente. On peut reproduire ce raisonnement avec un cercle centré sur l’un des points de la bordure :

On voit alors qu’il y a deux points d’intersection qui apparaissent. De quelle couleur sont ces points ? Ils ne peuvent pas être bleus mais il ne peuvent pas être roses non plus ! Il nous faut donc une troisième couleur.
Étape 2 : Simplifier le problème
Bon le problème étant déjà très simple, on peut se demander comment le simplifier encore davantage sans qu’il perde son sens. Pour l’instant on a un peu mieux compris comment la contrainte nous force à devoir utiliser plus de couleurs, mais on n’a pas encore du tout vu si même avec beaucoup de couleurs on s’en sortait. Simplifions nous donc la vie en oubliant le mot « minimum » dans la question, n’essayons pas de nous priver d’un nombre de couleurs. Bon n’allons pas non plus dans l’extrême en déclarant qu’on donne une couleur différente à chaque point du plan, on aimerait rester sur un nombre fini (ou au moins un nombre infini dénombrable pour les plus cultivés…).
Alors comment colorier le plan si on dispose de plein de couleurs ?
Vu que le plan est infini, il est bien d’avoir un motif. Le motif de cercle commencé précédemment était un peu compliqué à comprendre donc prenons le motif le plus simple possible. Par exemple, pavons le plan par des carrés.

Essayons de colorier ces carrés sans faire forcément de l’économie de couleur. Il va aussi falloir définir leur taille. Tout comme le raisonnement pour le cercle, il faut ici que la diagonale du carré soit de longueur ![]() pour que l’intérieur d’un carré ne pose pas de souci. En prenant
pour que l’intérieur d’un carré ne pose pas de souci. En prenant ![]() proche de
proche de ![]() , on voit qu’en utilisant par exemple
, on voit qu’en utilisant par exemple ![]() couleurs on a un coloriage qui respecte la contrainte.
couleurs on a un coloriage qui respecte la contrainte.

On a donc montré que ![]() couleurs sont suffisantes pour colorier le plan de cette façon. Notons
couleurs sont suffisantes pour colorier le plan de cette façon. Notons ![]() le nombre minimal qu’on cherche, appelé nombre chromatique du plan. En prenant en compte nos réflexions de l’étape 1, on a donc montré que
le nombre minimal qu’on cherche, appelé nombre chromatique du plan. En prenant en compte nos réflexions de l’étape 1, on a donc montré que
![]()
Étape 3 : Retour sur la borne inférieure
Revenons à la fin de l’étape ![]() . Si on examine ce qu’on a fait, on peut le résumer par le fait que si on trace un triangle équilatéral de côté
. Si on examine ce qu’on a fait, on peut le résumer par le fait que si on trace un triangle équilatéral de côté ![]() dans le plan, les sommets sont forcés d’avoir
dans le plan, les sommets sont forcés d’avoir ![]() couleurs différentes.
couleurs différentes.

On peut même en dire un peu plus d’après ce qu’on a fait. Supposons que nous pouvons colorier le plan avec uniquement ![]() couleurs. Alors on peut construire un losange, constitué de deux triangles équilatéraux, dont deux sommets opposés ont forcément la même couleur et cette couleur doit être différente des deux autres sommets.
couleurs. Alors on peut construire un losange, constitué de deux triangles équilatéraux, dont deux sommets opposés ont forcément la même couleur et cette couleur doit être différente des deux autres sommets.

On aimerait maintenant trouver une figure où l’un des sommets est forcé d’avoir une quatrième couleur, ce qui entraînerait une contradiction avec l’hypothèse qu’on peut colorier avec seulement ![]() couleurs et donc l’hypothèse serait fausse, il faudrait plus que
couleurs et donc l’hypothèse serait fausse, il faudrait plus que ![]() couleurs. Il s’agit d’un raisonnement par l’absurde.
couleurs. Il s’agit d’un raisonnement par l’absurde.
✏️ Nouvelle pause réflexion pour vous ici. C’est une étape non évidente où il faut réfléchir, tâtonner et il y a plusieurs idées possibles. Je vais en présenter une ici qui m’est venue après avoir réfléchi un certain temps.
Je rappelle qu’on suppose donc que nous disposons seulement de trois couleurs. On a alors vu, via le losange, qu’on peut forcer un point à avoir la même couleur qu’un autre. Mais on peut en fait forcer un grand nombre de points à avoir la même couleur qu’un point choisi en répétant le losange dans différentes directions.

On peut voir ça comme une rotation du losange autour du point choisi. Mais alors il est possible de tourner précisément le losange pour que deux points forcés se retrouvent à distance ![]() l’un de l’autre !
l’un de l’autre !

Ces deux points doivent alors avoir une couleur différente, contradiction ! Il nous faut donc au moins 4 couleurs !
Étape 4 : Retour sur la borne supérieure
Cette section est un peu plus compliquée que les autres à comprendre, mais accrochez-vous c’est intéressant !
On revient maintenant sur la borne supérieure car on sent bien qu’il est sans doute possible de l’améliorer. On a vraiment colorié un pavage basique (et qu’on a choisi de façon assez aléatoire) pour justifier que ![]() . Mais il y a plein d’autres pavages : triangulaire, hexagonal, avec n’importe quel polygone régulier, avec des cercles, etc. Quel pavage semble le plus adapté ?
. Mais il y a plein d’autres pavages : triangulaire, hexagonal, avec n’importe quel polygone régulier, avec des cercles, etc. Quel pavage semble le plus adapté ?
Pas évident de répondre à cette question, mais si on ne voit pas on peut juste essayer un par un les pavages en ajustant optimalement la taille du motif pour respecter la contrainte. Je vous laisse essayer de faire cela par vous-mêmes si vous êtes intéressés !
Je vais prendre une autre approche ici. On a vu qu’en prenant le pavage carré et en choisissant bien la taille des carrés on pouvait colorier le plan avec neuf couleurs. En fait il y avait pas mal de marge quand on a fait cela. Commençons donc déjà par être plus précis sur la taille des carrés qui convient.
Remarquons qu’il y a beaucoup de symétries dans le pavage carré et vu la façon symétrique dont on l’a colorié avec neuf couleurs, il nous suffit en fait de vérifier que pour un seul carré, il n’y a pas de problème (pas besoin de vérifier pour tous les carrés). Fixons donc notre attention sur un carré.

Comme expliqué plus haut, pour éviter qu’il y ait un problème au sein-même du carré, on doit avoir sa diagonale strictement inférieure à ![]() de longueur. Notons que par Pythagore (voir cet article pour un rappel 😉 ), le côté
de longueur. Notons que par Pythagore (voir cet article pour un rappel 😉 ), le côté ![]() du carré doit donc être strictement inférieur à
du carré doit donc être strictement inférieur à ![]() de longueur.
de longueur.
Ensuite on a des contraintes par tous les autres carrés violets autour de celui-ci. Par symétrie, il suffit de regarder la contrainte du carré violet situé à droite en diagonal et la contrainte du carré violet situé à droite. Puisque les diagonales sont plus longues que les côtés, la seule contrainte à regarder est en fait celle du carré violet situé à droite.

Il faut que lorsqu’on place notre bâton de longueur ![]() , ses extrémités ne puissent être sur les deux carrés en même temps. Il faut donc que
, ses extrémités ne puissent être sur les deux carrés en même temps. Il faut donc que ![]() c’est à dire que
c’est à dire que ![]() . Ainsi on peut choisir
. Ainsi on peut choisir ![]() comme on veut tant qu’il vérifie
comme on veut tant qu’il vérifie
![]()
On a donc une certaine marge de manœuvre. Notons que la borne supérieure va être compliqué à modifier puisqu’elle provient d’un problème au sein du carré. Dans l’idée, on va donc prendre ![]() le plus proche possible de
le plus proche possible de ![]() et plutôt jouer avec la borne inférieure.
et plutôt jouer avec la borne inférieure.
De plus on a vu que la contrainte des carrés violets en diagonal n’intervenait pas ici car celle des carrés horizontaux (et verticaux) domine. On peut donc s’amuser à rapprocher le carré en diagonal si cela nous permet de diminuer le nombre de couleurs. Concentrons nous sur une couleur et essayons de rapprocher le carré en diagonal. Rapprochons le d’une case en diagonal par exemple comme sur le dessin suivant.

On a alors deux problèmes qui se créent :
Problème 1 : La bordure
Les deux carrés en diagonal sont pile à une distance ![]() l’un de l’autre si
l’un de l’autre si ![]() … Et si
… Et si ![]() comme on en avait besoin, la distance entre les deux est
comme on en avait besoin, la distance entre les deux est ![]() ce qui pose encore plus problème… Mais en fait on est vraiment à la limite de ne pas avoir de problème. On avait jusque là laisser de côté la couleur du contour des carrés à la frontière mais il est temps de s’y intéresser et de la bricoler pour que tout fonctionne bien. Prenons notre loupe. Si on veut qu’un carré puisse avoir pile un côté égal à
ce qui pose encore plus problème… Mais en fait on est vraiment à la limite de ne pas avoir de problème. On avait jusque là laisser de côté la couleur du contour des carrés à la frontière mais il est temps de s’y intéresser et de la bricoler pour que tout fonctionne bien. Prenons notre loupe. Si on veut qu’un carré puisse avoir pile un côté égal à ![]() , on peut par exemple déclarer que toute sa bordure haute et sa bordure droite sont de même couleur que son intérieur, excepté le coin en haut à gauche et le coin en bas à droite. Le reste de sa bordure a des couleurs différentes, déterminées par la bordure haute et droite des carrés adjacents.
, on peut par exemple déclarer que toute sa bordure haute et sa bordure droite sont de même couleur que son intérieur, excepté le coin en haut à gauche et le coin en bas à droite. Le reste de sa bordure a des couleurs différentes, déterminées par la bordure haute et droite des carrés adjacents.

Cette décision résout non seulement le problème au sein même du carré mais surtout elle permet aussi que dans toutes les diagonales, nous n’ayons plus de problèmes.

Problème 2 : Le carré diagonal se rapproche du carré horizontal
L’autre problème qui était bien visible dans la figure est que si on rapproche le carré en diagonal droite du carré qu’on considère, il se rapproche aussi du carré à droite :
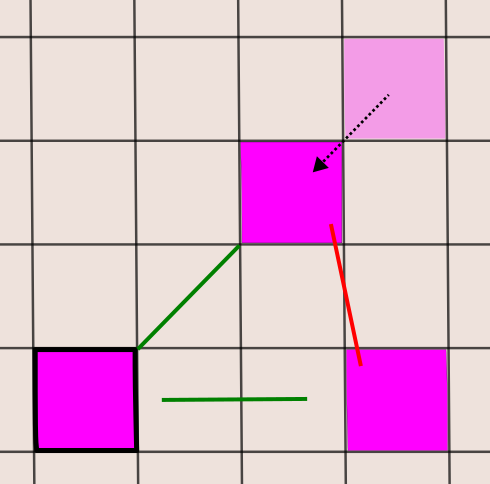
Une manière simple de résoudre ce problème est de repousser ce carré horizontal d’une case supplémentaire à droite.

Les deux problèmes étant résolus, on peut maintenant colorier notre plan avec cette nouvelle structure de couleur. Pour des raisons de lisibilité, on se souvient qu’on a réglé le problème des bordures même si on ne les dessine plus en détail. On a donc le coloriage suivant :

On voit qu’on a eu besoin de seulement ![]() couleurs, on a progressé !
couleurs, on a progressé !
Conclusion
On n’a pas fini de résoudre le problème et c’est déjà la conclusion ? Oui car en fait ce problème est encore ouvert de nos jours et, bien qu’il soit encore possible d’améliorer l’encadrement, je préfère attendre de voir si ça plait pour continuer cette histoire. Pour être précis, l’encadrement actuel connu est
![]()
Vous pouvez voir qu’il est possible d’améliorer précisément d’une unité chacune des bornes. J’explique très brièvement de quelle façon.
Amélioration de la borne inférieure
Elle a été améliorée à ![]() assez récemment, en 2018 par Aubrey de Grey, un biologiste de métier et mathématicien amateur. Cela montre que ce genre de problème est ouvert à tous ceux qui veulent y réfléchir et il est toujours possible de trouver des résultats même si d’autres mathématiciens professionnels y ont réfléchi avant nous !
assez récemment, en 2018 par Aubrey de Grey, un biologiste de métier et mathématicien amateur. Cela montre que ce genre de problème est ouvert à tous ceux qui veulent y réfléchir et il est toujours possible de trouver des résultats même si d’autres mathématiciens professionnels y ont réfléchi avant nous !
La preuve de De Grey est assistée par un ordinateur pour traiter de nombreux cas, elle reste malgré tout intéressante car elle nécessite de bonne idées pour se réduire à un nombre de cas à traiter.
Amélioration de la borne supérieure
Nous n’étions en fait plus très loin de montrer ![]() dans cet article mais il était déjà long donc j’ai préféré m’arrêter. Il y a deux façons connues de procéder :
dans cet article mais il était déjà long donc j’ai préféré m’arrêter. Il y a deux façons connues de procéder :
- On peut astucieusement continuer à jouer avec notre réseau carré en le bougeant un peu (je garde le suspens pour ceux qui veulent réfléchir…) et améliorer ainsi notre résultat.
- Une façon plus classique est de considérer le pavage hexagonal. En choisissant bien la taille des hexagones, on s’aperçoit que
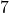 couleurs suffisent. Il s’agit en fait du meilleur pavage par polygone régulier (sans être modifié de façon astucieuse) qui permet cela. Mais ceci est une autre histoire…
couleurs suffisent. Il s’agit en fait du meilleur pavage par polygone régulier (sans être modifié de façon astucieuse) qui permet cela. Mais ceci est une autre histoire…
Si vous êtes intéressés d’en savoir plus, n’hésitez pas à me le faire savoir et j’écrirais peut être un nouvel article pour expliquer plus en détail les deux améliorations 🙂
Pour aller plus loin
Je donne ici les références que j’ai utilisées pour écrire cet article. Il y a un gros bouquin hyper complet sur le sujet écrit par Soifer. J’indique aussi l’article de De Grey qui a amélioré la borne inférieure.
- Bouquin de référence de Soifer : The Mathematical Coloring Book – Mathematics of Coloring and the Colorful Life of its Creators
- Article de Aubrey de Grey : The chromatic number of the plane is at least 5 (2018)