Kangourou des Maths – 4ème/3ème 2023 – Correction détaillée

Pour des conseils généraux sur le Kangourou des Mathématiques, cliquez là.

Je vous propose ici une correction détaillée de ce sujet du Kangourou des Mathématiques 2023 destiné aux élèves de 4ème/3ème. Vous pouvez retrouver d’autres sujets ainsi que toutes les infos sur le concours sur le site officiel du Kangourou.

✏️ A vous de jouer ! Cette correction n’a aucun intérêt si vous n’avez pas essayé de faire le sujet, alors faites-le avant ! Bon courage 🙂

Questions à 3 points

Question 1

Pour écrire un 2, elle utilise 5 allumettes. Pour écrire un 0, elle en utilise 6 et pour écrire un 3 elle en utilise 5. Donc pour écrire 2023, elle va en utiliser au total 5+6+5+5=21.

La réponse est donc B) 21.

Question 2

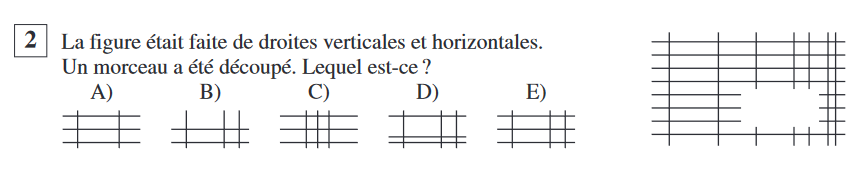
On essaye les possibilités, avec le nombre de lignes ainsi que leur espacement, on voit que seul le morceau E convient.

La réponse est donc E).

Question 3

En retournant 5 piles, Jean a alors 25 face et 25 pile.

La réponse est A) 5.

Question 4

Un trapèze est un quadrilatère dont deux côtés sont parallèles. Le triangle ne peut pas être partagé en deux trapèzes en traçant une ligne droite.

La réponse est donc A).

Question 5

Il s’agit de prolonger le trajet des auto-tamponneuses sur le schéma en s’aidant du quadrillage fourni. On voit alors qu’au bout de 10 secondes, les auto-tamponneuses 1 et 3 se rencontrent.

La réponse est donc B)1 et 3.

Question 6

On voit qu’entre les nombres des deux trous il y a 4 d’écart. Si on met un 8 dans le premier trou, on aura donc 8+4=12 dans l’autre trou et si on met un 8 dans le deuxième trou, on aura 8-4=4 dans l’autre trou.

La réponse est donc A) 4 ou 12.

Question 7

Notons x le nombre du sommet gauche de la figure. Le nombre du sommet haut sera alors 8-x. Celui à droite sera 9-(8-x)=1+x. Enfin celui en bas sera 13-(1+x)=12-x. Donc la somme qu’on cherche entre celui de gauche et celui du bas sera x+12-x=12.

La réponse est donc B) 12.

Une autre façon plus élégante et rapide d’obtenir la réponse m’a été proposée par un abonné, Anthony Aich : Il s’agit de remarquer que la somme totale des sommets fait 8+13=21. Le nombre x que l’on cherche vérifie donc 9+x=21 c’est-à-dire x=12.

Question 8

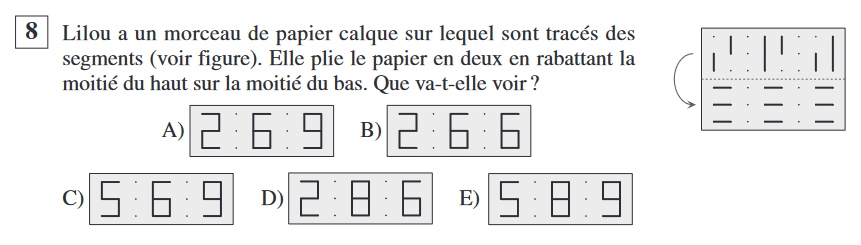
Il s’agit de bien visualiser ce qui se passe quand on replie. Les traits en haut passent en bas et inversement. Les traits à droite restent à droite et ceux à gauche restent à gauche.

La réponse est C) 569.

Questions à 4 points

Question 9

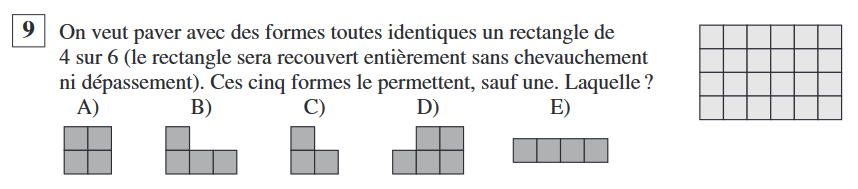
Le rectangle possède 4\times 6=24 carrés. Or la figure D possède 5 carrés et 5 ne divise pas 24, c’est donc impossible de réussir à paver avec cette figure.

La réponse est D).

Question 10

Il faut que le 1 soit avec le 8 sinon, sachant que le 3 et 4 sont déjà placés, la somme sera trop grande pour être atteinte. La somme des colonnes est donc 9, ce qui nous permet de compléter les deux cases de gauche avec 6 et 5. Puis on se sert de la somme des lignes pour savoir que le 7 va dans la case grisée (et le 2 dans celle de dessous).

La réponse est donc E) 7.

Question 11

Une arête est commune à exactement 2 faces. On peut donc au mieux couvrir les 6 faces avec 3 arêtes. On vérifie que cela est en effet possible (voir vidéo si besoin).

La réponse est donc B) 3.

Question 12

Notons r le rayon cherché et x la distance telle que 12+2x=2r (voir demi-disque du milieu). En regardant le demi-disque de gauche, on doit aussi avoir 22+x=2r. Finalement en résolvant cette équation, on trouve r=16.

La réponse est donc B) 16cm.

Question 13

En faisant le dessin, on voit que la distance x qu’on doit trouver est égale à l’hypoténuse d’un triangle rectangle. Ces deux autres côtés ont pour longueur 5-2=3 et 7-3=4. Par Pythagore, on trouve alors que x=5.

La réponse est donc C) 5km.

Question 14

On doit avoir 3 kangourou côte à côté. Pour minimiser le nombre de lièvres, on en place alors un immédiatement après, puis un kangourou pour respecter la contrainte que deux lièvres ne peuvent pas être à côté. Puis un lièvre, un kangourou et à nouveau un lièvre. On a donc un total de 5 kangourous dans la ronde.

La réponse est donc C) 5.

Question 15

Pour connaître le petit angle d’un fin losange, il suffit de regarder le centre de la figure et de voir que 10 angles de fin losange font un tour à 360°. L’angle d’un petit losange fait donc 36°. Puis on déduit le grand angle d’un gros losange en voyant que sur le bord de la figure, deux petits angles de fin losange et un grand angle d’un gros losange font 180°. On a donc le grand angle égal à 180-2\times 36=108°.

La réponse est donc B) 108°.

Question 16

En observant les centaines, on voit que le cœur suit le carré. Avec les dizaines, on voit que le triangle suit la croix. Et enfin avec les unités on voit que le carré suit le triangle.

La réponse est donc E).

Questions à 5 points

Question 17

Pour connaître les points situés à 5cm d’un sommet, il suffit de tracer un cercle de rayon 5 cm autour de ce sommet. Lorsque deux cercles s’intersectent, le point d’intersection est alors situé à 5cm des deux sommets correspondants. Il y a 4 points d’intersection à l’extérieur du carré, 4 à l’intérieur et il y aussi les 4 sommets du carré.

La réponse est donc E) 12.

Question 18

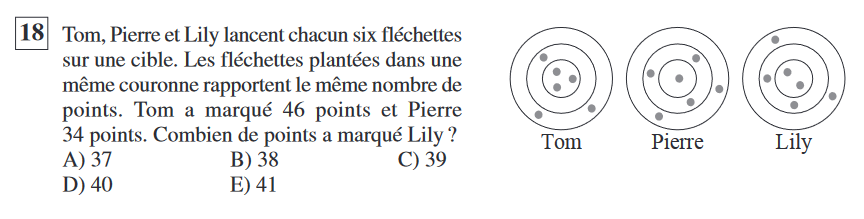
On note respectivement x,y,z la valeur de la couronne extérieure, du milieu et intérieur. On a les équations :

    \[2x + y +3z = 46\]

    \[2x +3y + z = 34\]

Le score de Lily est égal à 2x+2y+2z, ce qu’on peut obtenir en additionnant les deux lignes de notre système puis en le divisant par 2. On obtient alors 2x+2y+2z=(46+34)/2=40.

La réponse est donc D) 40.

Question 19

L’idée est que beaucoup d’entiers positifs vont venir se supprimer avec des entiers négatifs. En sommant de -1010 à 1012, on a 2023 termes dans la somme et tous se suppriment sauf 1011+1012=2023. La somme des chiffres de 1012 vaut 1+1+2=4.

La réponse est donc A) 4.

Question 20

En traçant la droite entre le milieu des segments [KR] et [NG] on obtient deux rectangles symétrique avec un la partie grisée qui est un triangle rectangle dans chacun d’eux. On peut tracer la hauteur issu de KN dans le triangle du haut (et celle issue de RG dans celui du bas) pour diviser la partie grisée en deux triangles rectangles qui correspondent exactement aux triangles de la partie non grisée.

L’aire de la partie blanche est donc égale à l’aire de la partie grise qui est 5\times (3\times 5)=75. Donc l’air du rectangle est 2\times 75=150.

La réponse est D) 150.

Question 21

Les chiffres 8 et 9 ne peuvent être adjacents qu’à 1. En observant la figure, cela signifie que la ligne du milieu est 9,1,8 (ou 8,1,9 ce qui est pareil par symétrie). Le 6 et le 7 ne peuvent être adjacents qu’à 1 et 2 donc on en déduit qu’en bas (ou en haut) on a 6,2,7. Enfin il nous reste 3,4 et 5. Le 5 ne peut être adjacent qu’à 1,2 et 3 donc on va devoir écrire en haut 4,3,5.

Le produit des cases grisés est alors 1\times 3\times 2 \times 8 \times 9= 6\times 72 = 432.

La réponse est donc C) 432.

Question 22

Prof a joué six parties, il a donc joué contre tous les autres nains, y compris Simplet. La seule partie de Grincheux est contre Prof. Joyeux a joué contre tout le monde sauf Grincheux, il a donc aussi joué avec Simplet. Les deux parties d’Atchoum sont contre Prof et Joyeux. Enfin il nous 2 parties à compter qui sont la partie de Timide contre Dormeur et de Timide contre Simplet. Finalement Simplet a joué 3 parties.

La réponse est C) 3.

Question 23

Il y a plus que 28 personnes dans la queue et le nombre de personnes N est un multiple de 3. Ce nombre ne peut pas être pair car sinon Martin ne pourrait pas avoir autant de personnes devant lui que derrière lui. De plus ce nombre ne peut pas être plus grand que 38 sinon l’ami à la 19ème place ne pourrait pas être derrière Martin. Finalement le seul nombre N qui fonctionne est donc 33 et on en déduit que Martin est à la 17ème place.

La réponse est donc D) 17.

Question 24

La phrase « en empruntant le chemin le plus court » signifie simplement que les souris se déplacent en ligne droite et donc sur les routes.

Notons x le nombre de souris qui vont du haut vers la gauche. On a alors 8-x souris qui vont du haut vers la droite. Donc 4-(8-x)=x-4 souris qui vont de gauche à droite. Donc 7-(x-4)=11-x souris qui vont de gauche vers le haut. On peut s’arrêter ici. On a x+11-x=11 souris qui ont emprunté le chemin marqué d’une flèche.

La réponse est donc B) 11.

Questions Bonus

Question 25

On commence par approche le plus 2023 en ajoutant des 777. On peut en ajouter deux : 777+777=1554. Il reste à obtenir 2023-1554=469. On l’approche le plus possible en ajoutant des 77, on trouve 77\times 6=385+77=462. Finalement 2023=777\times 2+ 77\times 6 +7. On a bien utilisé 19 fois le chiffre 7 et on a utilisé 6 fois le nombre 77.

La réponse est donc 6.

Question 26

En tâtonnant, on trouve qu’il y a exactement 3 façons de faire cette somme :

    \[17+18+19 = 54\]

    \[12+13+14+15=54\]

    \[2+3+4+5+6+7+8+9+10 = 54\]

Y-a-t-il une façon plus simple d’avoir ce résultat ?

La réponse est en tout cas 3.

Il y a en effet une façon plus rapide d’obtenir ce résultat, elle m’a été proposé par un abonné, clyp67. Il s’agit de remarquer que la moyenne d’une somme de k entiers consécutifs est un entier si k est impair et est \frac{1}{2} + un entier si k est pair. Il faut donc ici que \frac{54}{k} soit dans l’un de ces deux cas.

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *

Publications similaires