Le Théorème de Pythagore

Les chaussures sont un instrument pour marcher, les maths sont un instrument pour penser. On peut marcher sans chaussures, mais on va moins loin.

Jean-Marie Souriau

Le fameux théorème de Pythagore est certainement l’un des plus marquants de la scolarité. Même chez les allergiques aux maths, son énoncé reste pourtant plutôt bien connu. Que dit-il déjà ? Dans un triangle rectangle, le carré de la longueur du plus grand côté, appelé hypoténuse, est égale à la somme des carrés des longueurs des deux autres côtés. Très bien, mais qu’est-ce que cela signifie exactement et comment a-t-on pu trouver cela ? Oublions ce que nous savons quelques minutes et mettons nous dans la peau des Grecs de l’époque.

Le triangle est l’une des formes géométriques les plus simples. Il apparait naturellement en architecture : toits, escaliers, arches, etc. Si on veut construire un triangle, on trace deux traits et le troisième trait nous est ensuite imposé. La longueur de ce troisième trait semble donc liée à la longueur des deux premiers traits. Voici donc la question que l’on se pose :

❔ Peut-on déterminer la longueur du troisième côté d’un triangle quand on connaît la longueur des deux autres côtés ? Et si oui existe-il une formule ?

✏️ A vous de jouer ! N’hésitez pas à prendre une feuille de papier ou prenez au moins deux minutes de réflexion mentale pour ces questions.

Étape 1 : Comprendre la question

Disons qu’on me donne deux longueurs de côté. Je dessine un triangle ayant deux côtés de ces longueurs. On se rend compte que cela ne suffit pas. Il y a plusieurs triangles possibles.

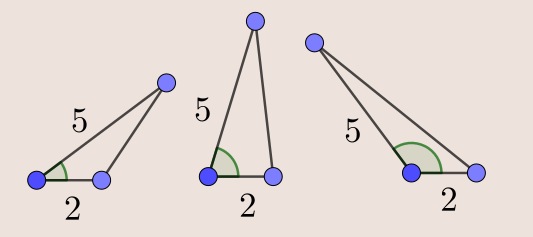
On voit qu’on peut en fait jouer avec l’angle entre les deux côtés pour créer plein de triangles valides. La longueur du troisième côté dépend de l’angle choisi. Il faut donc aussi spécifier cet angle pour avoir un unique triangle.

❔ J’ai dit cet angle mais si je spécifie un autre angle du triangle, est-ce que cela fonctionne encore ?

Je vous laisse faire pour vérifier que oui. J’ai donc besoin de deux longueurs et d’un angle pour être forcé de tracer le dernier côté d’une certaine façon. Vu que je n’ai qu’un choix, ce serait bien de pouvoir déterminer la longueur imposée. Comment vais-je donc pouvoir trouver une formule ?

Étape 2 : Simplifier la question

Avant de s’attaquer au problème dans son entièreté, il est déjà bon de voir si on arrive à le résoudre dans des cas plus simples. Si oui, cela pourra en plus nous donner des idées pour le résoudre de façon générale ensuite.

On a vu qu’on doit spécifier un angle, choisissons l’angle le plus simple possible. En général ce sont les valeurs extrêmes qu’on aime bien choisir, donc pour un angle ce serait 0 degré (« pas d’angle ») ou 180 degrés (l’angle plat). Le problème c’est que ça ne peut pas donner de triangle. Prenons donc ce qui parait être l’autre valeur la plus simple : l’angle de 90 degrés (angle droit).

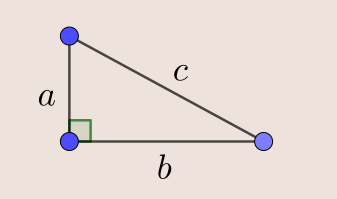
On se donne deux valeurs de côtés et . On pourrait prendre des valeurs particulières pour simplifier les choses mais on ne voit pas vraiment en quoi dire qu’elles valent 1 cm ou 2m changerait quelque chose. Par contre on peut simplifier en prenant ces deux valeurs égales : .

Étape 3 : S’attaquer au problème simplifié

Nous arrivons maintenant à l’étape difficile de résolution d’un problème : trouver une idée. Mais attention une idée ne sort pas du chapeau, il s’agit d’étudier le problème de différentes façons jusqu’à ce qu’elle surgisse. Cela demande un travail et il est tout à faire normal de ne pas trouver du premier coup ! Mon objectif est qu’au fur à mesure des articles, si vous avez du mal avec cette étape, vous sentiez malgré tout que c’est possible et que vous allez progresser.

Bon alors comment on fait ici ? Je ne sais pas vraiment mais il est toujours bienvenu de faire un bon gros dessin.

Le fait qu’on ait pris les deux côtés égaux me fait penser à la moitié d’un carré de côté . Si on le dessine on voit que le côté que l’on cherche est la diagonale de ce carré. Peut-on calculer cette diagonale ? Mmm c’est toujours la même question. En connaissant le côté d’un carré, on peut calculer son périmètre et son aire mais la diagonale c’est justement la formule qu’on cherche qui nous aiderait…

Ce serait bien si le côté pouvait être autre chose qu’une diagonale, s’il pouvait être lui aussi le côté d’un carré par exemple. Mais c’est possible en fait ! Je peux très bien tracer un carré de côté .

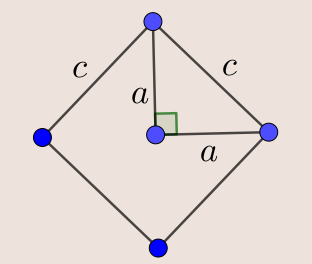
On remarque alors que le triangle est pile le quart de ce grand carré. On peut exactement le remplir de quatre triangles identiques ! L’aire des quatre triangles est donc égale à l’aire du grand carré.

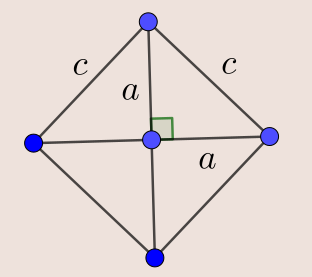
L’aire du grand carré vaut . L’aire d’un triangle vaut . L’aire des quatre triangles vaut donc . On a ainsi :

Donc

Super on a réussi à lier la longueur de l’hypoténuse à la longueur du côté , le problème simplifié est résolu !

A noter que j’ai pris la racine de l’équation sans paniquer pour enlever les carrés, mais les Grecs ont mis du temps à digérer l’existence de la racine de … On reparlera de cette racine une autre fois !

Étape 4 : Utiliser les idées acquises pour le problème général

Revenons maintenant au problème général avec potentiellement . Pour s’y attaquer, on essaye de voir si l’idée qu’on a développée dans la résolution du problème simplifié peut s’appliquer ici aussi. Construisons donc de la même façon un carré de côté .

Le triangle ne correspond plus exactement à un quart du carré… Mais ne soyons pas découragés pour si peu et essayons quand même de le remplir avec quatre triangles identiques du mieux possible. Après quelques essais pour le remplir du mieux possible avec des triangles identiques, on obtient le dessin suivant :

On voit qu’il reste juste un petit carré à l’intérieur. Donc l’aire du grand carré est égale à l’aire des quatre triangles l’aire du petit carré. Mais peut-on connaître l’aire du petit carré ? Pour cela il faudrait connaître la longueur d’un côté… Mais… Eurêka ! (bon ok personne ne dit ça) On la connaît en fait cette longueur ! En effet si on regarde bien, le côté du petit carré provient d’un côté de longueur du triangle auquel on retire un côté de longueur d’un autre triangle. La longueur d’un côté du petit carré est donc égale à . Ainsi

Et là magie ! On reconnaît le théorème de Pythagore ! Nous avons réussi !

Pour aller plus loin

• Nous avons traité le cas où le triangle est rectangle mais on sent bien qu’il devrait aussi exister une formule quand le triangle est plus général. Forcément cette formule dépendra alors d’un angle qu’on aura imposé. La formule existe bel et bien et porte le nom de formule d’Al-Kashi. Mais plutôt que de chercher immédiatement sur Google, je vous invite à la trouver par vous-mêmes si vous êtes intéressés.
• Il est aussi naturel de s’intéresser à la question dans l’autre sens : si jamais les côtés 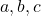d’un triangle vérifie l’égalité 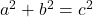alors est-ce que ce triangle est forcément rectangle ? La réponse est oui et cela s’appelle la réciproque du théorème de Pythagore que l’on voit aussi au collège. Soyez sûr de bien saisir la différence entre le théorème et sa réciproque et voyez si vous êtes capable de prouver la réciproque.

Voici la fin du tout premier article de ce blog ! J’espère que celui-ci vous aura plu. Je pense que mon style d’écriture est assez particulier et je suis très curieux des retours que je pourrais avoir, notamment des conseils sur comment m’améliorer. N’hésitez donc pas à m’en faire part 🙂 A la prochaine !